Berikut disajikan Latihan Soal untuk Persiapan menghadapi PAT tahun ajaran 2023 - 2024, silahkan disimak dan dipahami dengan baik setiap pembahasan yang ada agar memperoleh hasil yang maksimal saat PAT nanti.
Soal No 1
Jika dikatahui vektor $ \bar{a} ̅=(1,2,3)$ dan vektor $ \bar{b} ̅=(-1,-5,10)$, maka nilai dari $-2 \bar{a} + 3\bar{b}$ adalah ... .
a. $-5i-19j+24j$
b. $5i+19-24k$
c. $3i-j+24k$
d. $-5i,-15j+27k$
e. $5i+15j+27k$
a. $-5i-19j+24j$
b. $5i+19-24k$
c. $3i-j+24k$
d. $-5i,-15j+27k$
e. $5i+15j+27k$
Substitusikan nilai vektor ke persamaan yang diminta, maka
$\begin{align*} -2 \bar{a} + 3\bar{b} &= -2(1,2,3)+3(-1,-5,10)\\ &= (-2, -4, -6)+(-3,-15,30) \\ &= (-5,-19,24) \\ \end{align*}$
maka nilai dari $-2 \bar{a} + 3\bar{b} = (-5,-19,24)$ atau bisa juga ditulisakan dengan cara $-5i-19j+24k$
$\begin{align*} -2 \bar{a} + 3\bar{b} &= -2(1,2,3)+3(-1,-5,10)\\ &= (-2, -4, -6)+(-3,-15,30) \\ &= (-5,-19,24) \\ \end{align*}$
maka nilai dari $-2 \bar{a} + 3\bar{b} = (-5,-19,24)$ atau bisa juga ditulisakan dengan cara $-5i-19j+24k$
Soal No 2
Jika dikatahui titik $A(0,0,1), B(3,2,1)$ dan titik $C(-5,-3,4)$ maka nilai dari penjumlahan vektor $\bar{AB}+\bar{AC}$ adalah … .
a. $i-2j+3k$
b. $-2i-j+3k$
c. $-2i+j-2k$
d. $-i-j-3k$
e. $2i-j+3k$
a. $i-2j+3k$
b. $-2i-j+3k$
c. $-2i+j-2k$
d. $-i-j-3k$
e. $2i-j+3k$
Temukan lebih dulu vektor $\bar{AB}$ dan $\bar{AC}$ dengan cara
$\begin{align*} \bar{AB} &= B-A\\ &= (3,2,1)-(0,0,1) \\ &= (3,2,0) \\ \end{align*}$
$\begin{align*} \bar{AC} &= C-A\\ &= (-5,-3,4)-(0,0,1) \\ &= (-5,-3,3) \\ \end{align*}$
sehingga nilai dari $\bar{AB}+\bar{AC}$ adalah
$\begin{align*} \bar{AB}+\bar{AC} &= (3,2,0)+(-5,-3,3)\\ &= (-2,-1,3) \\ \end{align*}$
maka $\bar{AB}+\bar{AC}=(-2,-1,3)$ atau bisa juga ditulis $-2i-j+3k$
$\begin{align*} \bar{AB} &= B-A\\ &= (3,2,1)-(0,0,1) \\ &= (3,2,0) \\ \end{align*}$
$\begin{align*} \bar{AC} &= C-A\\ &= (-5,-3,4)-(0,0,1) \\ &= (-5,-3,3) \\ \end{align*}$
sehingga nilai dari $\bar{AB}+\bar{AC}$ adalah
$\begin{align*} \bar{AB}+\bar{AC} &= (3,2,0)+(-5,-3,3)\\ &= (-2,-1,3) \\ \end{align*}$
maka $\bar{AB}+\bar{AC}=(-2,-1,3)$ atau bisa juga ditulis $-2i-j+3k$
Soal No 3
Vektor satuan dari vektor $\bar{a}=-3j+4k$ adalah $\bar{c} ̅=mi+nj+ok$ maka temukanlah nilai dari $m+n+o$ … .
a. $\frac{1}{5}$
b. $-\frac{1}{5}$
c. $-\frac{2}{5}$
d. $\frac{4}{5}$
e. $\frac{3}{5}$
a. $\frac{1}{5}$
b. $-\frac{1}{5}$
c. $-\frac{2}{5}$
d. $\frac{4}{5}$
e. $\frac{3}{5}$
Temukan vektor satuan dari $\bar{a}$ dengan cara
$\begin{align*} \bar{c} &= \frac{1}{|\bar{a}|}\bar{a}\\ &= \frac{1}{\sqrt{0^2+(-3)^2+4^2}}.(-3j+4k)\\ &= \frac{1}{\sqrt{25}}.(-3j+4k)\\ &= \frac{1}{5}.(-3j+4k)\\ \end{align*}$
karena vektor satuan $\bar {a}$ adalah $\bar{c} =mi+nj+ok$ maka nilai dari $m=0, n=-\frac{3}{5}$ dan $o=\frac{4}{5}$, maka
$\begin{align*} m+n+o &= 0+ \left ( -\frac{3}{5}\right ) + \left ( \frac{4}{5}\right ) \\ &= \frac{1}{5} \end{align*}$
$\begin{align*} \bar{c} &= \frac{1}{|\bar{a}|}\bar{a}\\ &= \frac{1}{\sqrt{0^2+(-3)^2+4^2}}.(-3j+4k)\\ &= \frac{1}{\sqrt{25}}.(-3j+4k)\\ &= \frac{1}{5}.(-3j+4k)\\ \end{align*}$
karena vektor satuan $\bar {a}$ adalah $\bar{c} =mi+nj+ok$ maka nilai dari $m=0, n=-\frac{3}{5}$ dan $o=\frac{4}{5}$, maka
$\begin{align*} m+n+o &= 0+ \left ( -\frac{3}{5}\right ) + \left ( \frac{4}{5}\right ) \\ &= \frac{1}{5} \end{align*}$
Soal No 4
Jika vektor $\bar{a} ̅=3i-2j+ak$ tegak lurus dengan vektor $\bar{b} ̅=2i+2j-a$, maka nilai $a$ yang memenuhi adalah … .
a. $\sqrt{2}$
b. $-\sqrt{2}$
c. $\sqrt{2}$ dan $-\sqrt{2}$
d. $0$
e. $\sqrt{3}$
a. $\sqrt{2}$
b. $-\sqrt{2}$
c. $\sqrt{2}$ dan $-\sqrt{2}$
d. $0$
e. $\sqrt{3}$
Ingat bahwa jika dua buah vektor saling tegak lurus, maka hasil kalinya adalah 0, sehingga
$\begin{align*} \bar{a}.\bar{b} &= 0 \\ (3,-2,a).(2,2,-a) &= 0\\ 6 + (-4) +(-a^2) &= 0 \\ (-a^2) &= -2 \\ a &= \pm \sqrt{2} \\ \end{align*}$
$\begin{align*} \bar{a}.\bar{b} &= 0 \\ (3,-2,a).(2,2,-a) &= 0\\ 6 + (-4) +(-a^2) &= 0 \\ (-a^2) &= -2 \\ a &= \pm \sqrt{2} \\ \end{align*}$
Soal No 5
Perhatikan gambar berikut!
Nyatakanlah vektor $\bar{AB}$ ke dalam vektot $\bar{a}$ dan vektor $\bar{b}$ jika $\bar{a}=\bar{AD}$ dan $\bar{b}=\bar{AC}$ ... .
a. $\bar{a} + \bar{b}$
b. $\bar{a} - \bar{b}$
c. $\bar{b} - \bar{a}$
d. $\bar{a} - 2\bar{b}$
e. $\bar{b} + 2\bar{a}$
a. $\bar{a} + \bar{b}$
b. $\bar{a} - \bar{b}$
c. $\bar{b} - \bar{a}$
d. $\bar{a} - 2\bar{b}$
e. $\bar{b} + 2\bar{a}$
karena kita diminta untuk menyatakan vektor $\bar{AB}$, maka cobalah tarik vektor yang pangkalnya di titik $A$ ke salah satu titik yang ada pada persegi. Misalnya kita ambil titik $C$, kemudian dari $C$ tarik ke titik $B$ yang merupakan ujung vektor $\bar{AB}$, sehingga karena $\bar{a}=\bar{AD}=-\bar{CB}$ dan $\bar{b}=\bar{AC}$
$\begin{align*} \bar{AB} &= \bar{AC}+\bar{AD} \\ &= \bar{AC}+(-\bar{CB})\\ &= \bar{b}+(-\bar{a}) \\ &= \bar{b} -\bar{a} \\ \end{align*}$
$\begin{align*} \bar{AB} &= \bar{AC}+\bar{AD} \\ &= \bar{AC}+(-\bar{CB})\\ &= \bar{b}+(-\bar{a}) \\ &= \bar{b} -\bar{a} \\ \end{align*}$
Soal No 6
Jika $\bar{a}=2i-xj+2yk$ sejajar dengan vektor $\bar{b}=i-(1+x)j+(2y-x)k$, maka berapakah nilai dari $x+y$ adalah … .
a. 0
b. -2
c. 2
d. 4
e. -4
a. 0
b. -2
c. 2
d. 4
e. -4
karena dua vektor sejajar, maka akan berlaku
$\begin{pmatrix} 2 \\ -x \\ 2 \end{pmatrix} = k \begin{pmatrix} 1\\ -(1+x) \\ (2y-x)\end{pmatrix}$
sehingga haruslah menemukan nilai $k$ kemudian $x$ dan $y$
Cari $k$
$\begin{align*} 2 &= k.1 \\ k &= 2\\ \end{align*}$
Cari $x$
$\begin{align*} -x &= -k(1+x) \\ -x &= -2(1+x) \\ -x &= -2-2x) \\ -x+2x &= -2 \\ x &= -2\\ \end{align*}$
Cari $y$
$\begin{align*} 2y &= k(2y-x) \\ 2y &= 2(2y-(-2)) \\ 2y &= 4y+4) \\ 2y-4y &= 4 \\ y &= -2\\ \end{align*}$
maka nilai dari $x+y=(-2)+(-2)=-4$
$\begin{pmatrix} 2 \\ -x \\ 2 \end{pmatrix} = k \begin{pmatrix} 1\\ -(1+x) \\ (2y-x)\end{pmatrix}$
sehingga haruslah menemukan nilai $k$ kemudian $x$ dan $y$
Cari $k$
$\begin{align*} 2 &= k.1 \\ k &= 2\\ \end{align*}$
Cari $x$
$\begin{align*} -x &= -k(1+x) \\ -x &= -2(1+x) \\ -x &= -2-2x) \\ -x+2x &= -2 \\ x &= -2\\ \end{align*}$
Cari $y$
$\begin{align*} 2y &= k(2y-x) \\ 2y &= 2(2y-(-2)) \\ 2y &= 4y+4) \\ 2y-4y &= 4 \\ y &= -2\\ \end{align*}$
maka nilai dari $x+y=(-2)+(-2)=-4$
Soal No 7
Vektor proyeksi $\bar{a} ̅=(4,1,-4 \sqrt{3})$ pada $\bar{b}=(3,0,-\sqrt{3})$ adalah … .
a. $-3i-j+ √3 k$
b. $-3i+j+ k$
c. $-3i+ 2√3 j$
d. $-3i- 2√3 k$
e. $6i- 2√3 k$
a. $-3i-j+ √3 k$
b. $-3i+j+ k$
c. $-3i+ 2√3 j$
d. $-3i- 2√3 k$
e. $6i- 2√3 k$
dengan menggunkan rumus vektor proyeksi $\bar{a}$ pada $\bar{b}$ dan misalkan vektornya adalah $\bar{c}$ maka diperoleh
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|^2}. \bar{b} \\ &= \frac{(4,1,-4 \sqrt{3}).(3,0,-\sqrt{3})}{(\sqrt{3^2+0^2+(-\sqrt{3})^2})^2}. (3,0,-\sqrt{3}) \\ &= \frac{12+0+12}{(\sqrt{9+0+3})^2}. (3,0,-\sqrt{3}) \\ &= \frac{24}{12}. (3,0,-\sqrt{3}) \\ &= 2. (3,0,-\sqrt{3}) \\ &= (6,0,-2\sqrt{3}) \\ \end{align*}$
sehingga proyeksi $\bar{a}$ pada $\bar{b}$ adalag $(6,0,-2\sqrt{3})$ atau $6i -2\sqrt{3}k$
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|^2}. \bar{b} \\ &= \frac{(4,1,-4 \sqrt{3}).(3,0,-\sqrt{3})}{(\sqrt{3^2+0^2+(-\sqrt{3})^2})^2}. (3,0,-\sqrt{3}) \\ &= \frac{12+0+12}{(\sqrt{9+0+3})^2}. (3,0,-\sqrt{3}) \\ &= \frac{24}{12}. (3,0,-\sqrt{3}) \\ &= 2. (3,0,-\sqrt{3}) \\ &= (6,0,-2\sqrt{3}) \\ \end{align*}$
sehingga proyeksi $\bar{a}$ pada $\bar{b}$ adalag $(6,0,-2\sqrt{3})$ atau $6i -2\sqrt{3}k$
Soal No 8
Panjang proyeksi vektor $\bar{a}=(-2,1,2)$ pada $\bar{b} =(-2,1,2)$ adalah … .
a. 0
b. 1
c. 2
d. 3
e. 4
a. 0
b. 1
c. 2
d. 3
e. 4
dengan menggunkan rumus panjang vektor proyeksi $\bar{a}$ pada $\bar{b}$ dan misalkan vektornya adalah $\bar{c}$ maka diperoleh
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|}\\ &= \frac{(-2,1,2).(-2,1,2)}{\sqrt{(-2)^2+1^2+2^2}}\\ &= \frac{4+1+4}{\sqrt{9}}\\ &= \frac{9}{3}\\ &= 3\\ \end{align*}$
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|}\\ &= \frac{(-2,1,2).(-2,1,2)}{\sqrt{(-2)^2+1^2+2^2}}\\ &= \frac{4+1+4}{\sqrt{9}}\\ &= \frac{9}{3}\\ &= 3\\ \end{align*}$
Soal No 9
Jika panjang proyeksi vektor$\bar{a}=(-1,0,x)$ pada $\bar{b}=(0,1,\sqrt{8})$ adalah $2\sqrt{18}$ , maka berapakah nilai $x$ yang memenuhi …. .
a. -3
b. 0
c. 3
d. 9
e. 6
a. -3
b. 0
c. 3
d. 9
e. 6
dengan menggunkan rumus panjang vektor proyeksi $\bar{a}$ pada $\bar{b}$ dan misalkan vektornya adalah $\bar{c}$ maka diperoleh
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|}\\ 2\sqrt{18} &= \frac{(-1,0,x).(0,1,\sqrt{8})}{\sqrt{0^2+1^2+\sqrt{8}^2}}\\ 2\sqrt{9.2} &= \frac{0+0+\sqrt{4.2}.x}{\sqrt{9}}\\ 2.3\sqrt{2} &= \frac{2\sqrt{2}.x}{3}\\ 3.2.3\sqrt{2}&= 2\sqrt{2}.x .......... (\text{sederhanakan})\\ 9 &= x \\ \end{align*}$
$\begin{align*} \bar{c} &= \frac{\bar{a}.\bar{b}}{|\bar{b}|}\\ 2\sqrt{18} &= \frac{(-1,0,x).(0,1,\sqrt{8})}{\sqrt{0^2+1^2+\sqrt{8}^2}}\\ 2\sqrt{9.2} &= \frac{0+0+\sqrt{4.2}.x}{\sqrt{9}}\\ 2.3\sqrt{2} &= \frac{2\sqrt{2}.x}{3}\\ 3.2.3\sqrt{2}&= 2\sqrt{2}.x .......... (\text{sederhanakan})\\ 9 &= x \\ \end{align*}$
Soal No 10
Jika dikatahui vektor $\bar{a}=(1,0,1)$ dan vektor $b=(0,1,1)$, maka besar sudut antara vektor $\bar{a}$ dan $\bar{b}$ adalah … .
a. $30°$
b. $45°$
c. $60°$
d. $90°$
e. $120°$
a. $30°$
b. $45°$
c. $60°$
d. $90°$
e. $120°$
Untuk menemukan sudut antar dua vektor dapat ditemukan dengan cara sebagai berikut
$\begin{align*} cos(\alpha) &= \frac{\bar{a}.\bar{b}}{|\bar{a}|.|\bar{b}|} \\ cos(\alpha) &= \frac{(1,0,1).(0,1,1)}{\sqrt{1^2+0^2+1^2}.\sqrt{0^2+1^2+1^2}} \\ cos(\alpha) &= \frac{0+0+1}{\sqrt{2}.\sqrt{2}} \\ cos(\alpha) &= \frac{1}{2} \\ \end{align*}$
maka agar $cos(\alpha)=\frac{1}{2}$, maka haruslah $\alpha = 60°$
$\begin{align*} cos(\alpha) &= \frac{\bar{a}.\bar{b}}{|\bar{a}|.|\bar{b}|} \\ cos(\alpha) &= \frac{(1,0,1).(0,1,1)}{\sqrt{1^2+0^2+1^2}.\sqrt{0^2+1^2+1^2}} \\ cos(\alpha) &= \frac{0+0+1}{\sqrt{2}.\sqrt{2}} \\ cos(\alpha) &= \frac{1}{2} \\ \end{align*}$
maka agar $cos(\alpha)=\frac{1}{2}$, maka haruslah $\alpha = 60°$
Soal No 11
Jika diketahui dua buah vektor $|\bar{a} |=1, |\bar{b} |=3$ dan $|\bar{a}-\bar{b} |=\sqrt{12}$, maka berapakah besar cosinus sudut yang dibentuk oleh kedua vektor tersebut … .
a. $\frac{1}{3}$
b. $-\frac{1}{3}$
c. $0$
d. $\frac{1}{2}$
e. $-\frac{1}{2}$
a. $\frac{1}{3}$
b. $-\frac{1}{3}$
c. $0$
d. $\frac{1}{2}$
e. $-\frac{1}{2}$
Dengan menggunkan rumus panjang selisih vektor maka diperoleh.
$\begin{align*} |\bar{a}-\bar{b}|^2 &= |\bar{a}|^2+|\bar{b}|^2-2.|\bar{a}|.|\bar{b}|.cos(\alpha) \\ \sqrt{12}^2 &= 1^2+3^2-2.1.3.cos(\alpha) \\ 12 &= 1+9-6.cos(\alpha) \\ 12-10 &=-6.cos(\alpha) \\ 2 &=-6.cos(\alpha) \\ \frac{2}{-6} &= cos(\alpha) \\ -\frac{1}{3} &= cos(\alpha) \end{align*}$
$\begin{align*} |\bar{a}-\bar{b}|^2 &= |\bar{a}|^2+|\bar{b}|^2-2.|\bar{a}|.|\bar{b}|.cos(\alpha) \\ \sqrt{12}^2 &= 1^2+3^2-2.1.3.cos(\alpha) \\ 12 &= 1+9-6.cos(\alpha) \\ 12-10 &=-6.cos(\alpha) \\ 2 &=-6.cos(\alpha) \\ \frac{2}{-6} &= cos(\alpha) \\ -\frac{1}{3} &= cos(\alpha) \end{align*}$
Soal No 12
Diketahui titik titik $C$ yang berada diantara titik $A(0,-1,-4)$ dan titik $B(-5,4,-9)$, sehingga memenuhi perbandingan $AC : CB$ adalah $2 : 3$, maka temukanlah vektor posisi $C$ … .
a. $-2i+j+ 6k$
b. $-2i-j+ 6k$
c. $-2i-j- 6k$
d. $-2i+j- 6k$
e. $3i+j+ 6k$
a. $-2i+j+ 6k$
b. $-2i-j+ 6k$
c. $-2i-j- 6k$
d. $-2i+j- 6k$
e. $3i+j+ 6k$
ilustrasikan soal ke dalam gambar kemudian dengan menggunkan perbandingan vektor maka akan diperoleh hubungan titiknya yaitu.
$\begin{align*} C &= \frac{A.3+B.2}{5} \\ C &= \frac{(0,-1,-4).3+(-5,4,-9).2}{5} \\ C &= \frac{(0,-3,-12)+(-10,8,-18)}{5} \\ C &= \frac{(-10,5,-30)}{5} \\ C &= (-2,1,-6) \\ \end{align*}$
$\begin{align*} C &= \frac{A.3+B.2}{5} \\ C &= \frac{(0,-1,-4).3+(-5,4,-9).2}{5} \\ C &= \frac{(0,-3,-12)+(-10,8,-18)}{5} \\ C &= \frac{(-10,5,-30)}{5} \\ C &= (-2,1,-6) \\ \end{align*}$
Soal No 13
Coba perhatikan beberapa vektor berikut. Vektor yang memiliki arah dan besar yang sama adalah
a. $\bar{a}$ dan $\bar{b}$
b. $\bar{a}$ dan $\bar{c}$
c. $\bar{a}$ dan $\bar{d}$
d. $\bar{a}$ dan $\bar{e}$
e. tidak ada
b. $\bar{a}$ dan $\bar{c}$
c. $\bar{a}$ dan $\bar{d}$
d. $\bar{a}$ dan $\bar{e}$
e. tidak ada
untuk menemukan vaktor yang memiliki arah yang sama, maka hitung banyak kotak yang vertikal dan horizontal dari pangkal hingga ujung vektornya. Maka dia akan searah jika banyak kotak yang vertikal dan horizontal sama atau berkelipatan.
kemudian untuk melihat apakah besarnya sama maka banyak kotaknya dari ujung ke pangkah vektor harus sama.
maka dengan kosep tersebut, jelas sekali vektor yang memiliki arah dan besar yang sama "tidak ada"
kemudian untuk melihat apakah besarnya sama maka banyak kotaknya dari ujung ke pangkah vektor harus sama.
maka dengan kosep tersebut, jelas sekali vektor yang memiliki arah dan besar yang sama "tidak ada"
Soal No 14
Data Statistika yang terdiri dari satu buah varibel kuantitatif disebut dengan … .
a. Univariat
b. Bivariat
c. Multivariat
d. Kuantitatif
e. Kualitatif
a. Univariat
b. Bivariat
c. Multivariat
d. Kuantitatif
e. Kualitatif
Univariat = Data Statistika yang terdiri dari satu buah varibel
Bivariat= Data Statistika yang terdiri dari dua buah varibel
Multivariat= Data Statistika yang terdiri dari banyak buah varibel
Kuantitatif = Data Statistika yang berupa data angka
Kualitatif = Data Statistika yang berupa data verbal / tulisan
Bivariat= Data Statistika yang terdiri dari dua buah varibel
Multivariat= Data Statistika yang terdiri dari banyak buah varibel
Kuantitatif = Data Statistika yang berupa data angka
Kualitatif = Data Statistika yang berupa data verbal / tulisan
Soal No 15
Adi ingin mengetahui Pengaruh porsi latihan dengan prestasi yang diperoleh seorang atlet sepak bola. Maka yang merupakan variabel bebas adalah ? apakah posisinya di sumbu x atau sumbu y ?
a. Porsi latihan, sumbu x
b. Porsi latihan, sumbu y
c. Prestasi , sumbu x
d. Prestasi , sumbu y
e. Atlet, sumbu x
a. Porsi latihan, sumbu x
b. Porsi latihan, sumbu y
c. Prestasi , sumbu x
d. Prestasi , sumbu y
e. Atlet, sumbu x
Ciri dari variabel bebas adalah variabel yang memepenaruhi variabel lainnya dan umumnya letaknya di sumbu y. Dalam soal jelas sekali bahwa porsi latihan sangat mempengarhui prestasi seorang atlet tersebut. Sehingga jika data di soal disajikan dalam bentuk diagram pencar maka porsi latihan akan terletak di sumbu y.
Soal No 16
perhatikan sebaran data beikut !
a. Semakin tinggi tinggi tinggi badan maka akan semakin rendah prestasi
b. Semakin rendah tinggi tinggi maka akan semakin tinggi prestasi
c. Semakin rendah tinggi tinggi tinggi maka akan semakin rendah prestasi
d. Semakin tinggi tinggi tinggi tinggi maka akan semakin tinggi prestasi
e. Tidak ada Hubungan
a. Semakin tinggi tinggi tinggi badan maka akan semakin rendah prestasi
b. Semakin rendah tinggi tinggi maka akan semakin tinggi prestasi
c. Semakin rendah tinggi tinggi tinggi maka akan semakin rendah prestasi
d. Semakin tinggi tinggi tinggi tinggi maka akan semakin tinggi prestasi
e. Tidak ada Hubungan
Perhatikan sebaran data yang disajikan di dalam soal, terlihat jelas sebaran datanya sangat tidak teratur dan tidak memiliki pola tertentu sehingga dapat disimpulkan data tidak memiliki korelasi atau tidak ada hubungan antara variabel bebas dan variabel terikatnya.
Soal No 17
Perhatikan data berikut ini!
maka dengan menggambar diagram pencarnya, jenis korelasi yang cocok adalah … .
a. Positif dengan korelasi lemah
b. Positif dengan korelasi kuat
c. Negatif dengan korelasi lemah
d. Negatif dengan korelasi kuat
e. Tidak ada korelasi
a. Positif dengan korelasi lemah
b. Positif dengan korelasi kuat
c. Negatif dengan korelasi lemah
d. Negatif dengan korelasi kuat
e. Tidak ada korelasi
Jika data diatas disajikan ke dalam diagram pencar, maka akan diperoleh bentuk sebagai berikut
terlihat jelas bahwa, data memiliki korelasi negatif karena garis regreseinya turun, kemudian jika dilihat jarak titik-titik dengan garis regresinya sangat dekat, maka regresi tersebut tergolong ke korelasi yang kuat.
Soal No 18
Perhatikan Diagram pencar berikut ini !
Data tabel yang cocok dengan gambar diatas adalah …
a.
b.
c.
d.
e.
a.
b.
c.
d.
e.
Ujilah jawaban dengan gambar diagramnya, misal diambil jawaban A, maka coba cocokan data variavel $x$ dan variabel $y$ dalam gambar diagramnya jika cocok maka langsung itu jawabanya, dan jika hanya satu data yang berbeda maka ujilah jawaban lain sehingga semua data cocok.
Soal No 19
Diketahui data sebagai berikut.
Persamaan garis regresi yang cocok dengan data diatas adalah …
a. $y=\frac{1}{2}x+\frac{5}{2}$
b. $y=\frac{1}{2}x-\frac{5}{2}$
c. $y=-\frac{1}{2}x+\frac{5}{2}$
d. $y=-\frac{4}{7}x+\frac{11}{4}$
e. $y=\frac{4}{7}x-\frac{19}{3}$
a. $y=\frac{1}{2}x+\frac{5}{2}$
b. $y=\frac{1}{2}x-\frac{5}{2}$
c. $y=-\frac{1}{2}x+\frac{5}{2}$
d. $y=-\frac{4}{7}x+\frac{11}{4}$
e. $y=\frac{4}{7}x-\frac{19}{3}$
Temukan terlebih dahulu rata-rata datanya dengan cara :
$\bar{x}=\frac{15}{5}=3$
$\bar{y}=\frac{20}{5}=4$
kemudian temykan nilai $a$ dan $b$ dengan melengkapi tabel berikut.
maka nilai $b$ diperoleh dengan cara
$\begin{align*} b &= \frac{SS_{xy}}{SS_{xx}} \\ &= \frac{7}{14} \\ &= \frac{1}{2} \\ \end{align*}$
kemudian nilai $a$ diperoleh dengan cara
$\begin{align*} \bar{y} &= a + b \bar{x} \\ 4 &= a+\frac{1}{2}.3 \\ 4-\frac{3}{2} &= a \\ a &=\frac{5}{2} \\ \end{align*}$
maka persamaan garis regresinya adalah
$y=\frac{1}{2}x+\frac{5}{2}$
$\bar{x}=\frac{15}{5}=3$
$\bar{y}=\frac{20}{5}=4$
kemudian temykan nilai $a$ dan $b$ dengan melengkapi tabel berikut.
$\begin{align*} b &= \frac{SS_{xy}}{SS_{xx}} \\ &= \frac{7}{14} \\ &= \frac{1}{2} \\ \end{align*}$
kemudian nilai $a$ diperoleh dengan cara
$\begin{align*} \bar{y} &= a + b \bar{x} \\ 4 &= a+\frac{1}{2}.3 \\ 4-\frac{3}{2} &= a \\ a &=\frac{5}{2} \\ \end{align*}$
maka persamaan garis regresinya adalah
$y=\frac{1}{2}x+\frac{5}{2}$
Soal No 20
Sesuai soal No 19, menurut nilai koefisient product momentnya maka data akan tergolong ke dalam korelasi …
a. Tidak ada korelasi
b. Lemah
c. Sedang
d. Kuat
e. Sempurna
a. Tidak ada korelasi
b. Lemah
c. Sedang
d. Kuat
e. Sempurna
Lengkapilah tabel seperti soal pada no 19, sehingga diperoleh tabel sebagai berikut.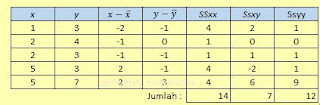
maka untuk menemukan korelasi data, temukan nilai $r$ dengan cara
$\begin{align*} r &= \frac{SS_{xy}}{\sqrt{SS_{xx}.SS_{xy}}} \\ &=\frac{7}{\sqrt{14.12}} \\ &= \frac{7}{\sqrt{168}} \\ &= \frac{7}{12,96} \\ &= 0,54 \\ \end{align*}$
karena nilai $r=0,45$ maka sesuai tabel pada materi Korelasi Product Moment, maka korelasi data termasuk di korelasi sedang
maka untuk menemukan korelasi data, temukan nilai $r$ dengan cara
$\begin{align*} r &= \frac{SS_{xy}}{\sqrt{SS_{xx}.SS_{xy}}} \\ &=\frac{7}{\sqrt{14.12}} \\ &= \frac{7}{\sqrt{168}} \\ &= \frac{7}{12,96} \\ &= 0,54 \\ \end{align*}$
karena nilai $r=0,45$ maka sesuai tabel pada materi Korelasi Product Moment, maka korelasi data termasuk di korelasi sedang
Soal No 21
Sesuai soal No 19. Berapa persen tingkat korelasi variabel x dan y sesuai dengan nilai dari koefisien determinasinya … .
a. 29,17 %
b. 28,40 %
c. 27,6 %
d. 26,52%
e. 25,9%
a. 29,17 %
b. 28,40 %
c. 27,6 %
d. 26,52%
e. 25,9%
Langkah untuk menemukan tingkat korelasinya sama dengan soal di nomor 20, yaitu hanya perlu mengkuadratkan hasil $r$ dan kalikan dengan 100 %, maka diperoleh
$\begin{align*} r^2 &= 0.54^2 \\ &= 0,2916\\ \end{align*}$
maka jika dikalikan 100 %, maka $r^2=29,16$% atau $r^2=29,17$% jika dibulatkan.
$\begin{align*} r^2 &= 0.54^2 \\ &= 0,2916\\ \end{align*}$
maka jika dikalikan 100 %, maka $r^2=29,16$% atau $r^2=29,17$% jika dibulatkan.
Soal No 22
Perhatikan Gambar berikut
Jika persamaan garis regresi data tersebut adalah y = 0.27x + 3.67 maka berpakah banyak uang saku $(x)$ dimas jika ia menginginkan tabungan $(y)$ sebanyak 10 … .
a. 34,13
b. 23,44
c. 23,67
d. 23,55
e. 23
a. 34,13
b. 23,44
c. 23,67
d. 23,55
e. 23
Untuk menemukan banyak perkiraan tabunganya, kita hanya perlu mensubstitusi nilai $y=10$ ke persamaannya sehingga diperoleh.
$\begin{align*} y &= 0.27x + 3.67 \\ 10 &= 0.27x + 3.67 \\ 10-3.67 &= 0.27x \\ \frac{6,33}{0.27} &= x \\ x &= 23,44 \\ \end{align*}$
$\begin{align*} y &= 0.27x + 3.67 \\ 10 &= 0.27x + 3.67 \\ 10-3.67 &= 0.27x \\ \frac{6,33}{0.27} &= x \\ x &= 23,44 \\ \end{align*}$
Soal No 23
Perhatikan data berikut ini
Dari gambar diatas, yang memiliki korelasi paling kuat adalah ..
a. Gambar a
b. Gambar b
c. Gambar c
d. Gambar d
e. Semua sama
a. Gambar a
b. Gambar b
c. Gambar c
d. Gambar d
e. Semua sama
Untuk menemukan jenis korelasi dari suatu gambar diagram pencar, maka lihat kerapatan titik-titiknya dengan suatu garis. jika semakin rapat maka akan semakin kuat, dan jika semakin jauh maka akan semakin lemah.
Soal No 24
Manakah dari pernyataan berikut yang memiliki korelasi positif … .
a. Pengaruh prestasi terhadap jenis kelamin
b. Pengaruh banyak uang dengan kebahagiaan seseorang
c. Pengaruh banyak pohon dengan polusi udara
d. Pengaruh banyaknya air dengan waktu yang diperlukan memanaskannya
e. Pengaruh banyak pakian dengan suhu tubuh
a. Pengaruh prestasi terhadap jenis kelamin
b. Pengaruh banyak uang dengan kebahagiaan seseorang
c. Pengaruh banyak pohon dengan polusi udara
d. Pengaruh banyaknya air dengan waktu yang diperlukan memanaskannya
e. Pengaruh banyak pakian dengan suhu tubuh
Korelasi positif adalah korelasi yang jika variabel bebasnya meingkat $(x)$ maka variabel terikatnya $(y)$ juga akan ikut meningkat, maka dalam soal jelas sekali bahwa semakin banyak air yang dipanaskan maka akan semakin banyak waktu yang diperlukan.
Soal No 25
Adi mendapatkan data sebagai berikut.
Maka variabel bebas yang di teliti adi memiliki tingkat korelasi sebesar a %, maka berapa persenkah pengaruh variabel lainnya … .
a. 0 %
b. 25 %
c. 50 %
d. 75 %
e. 100 %
a. 0 %
b. 25 %
c. 50 %
d. 75 %
e. 100 %
Sama seperti soal no 21, yaitu akan ditemukan nilai $r$ dengan cara menemukan tabel berikut terlebih dahulu.
$\begin{align*} r &= \frac{SS_{xy}}{\sqrt{SS_{xx}.SS_{xy}}} \\ &=\frac{2}{\sqrt{2.2}} \\ &= \frac{2}{\sqrt{4}} \\ &= \frac{2}{2} \\ &= 1 \\ \end{align*}$
maka jika dikalikan 100 %, maka $r^2=100$% yang memiliki makna bahwa pengaruh variabel bebas terhadap variabel terikatnya adalah 100 %, sehingga jika ditanyakan pengaruh variabel lainnya akan diperoleh dengan cara 100 % di kurangi dengan hasil $r$, sehingga diperoleh pengaruh variabel lainnya adalah $(100-100)$% = 0 %
$\begin{align*} r &= \frac{SS_{xy}}{\sqrt{SS_{xx}.SS_{xy}}} \\ &=\frac{2}{\sqrt{2.2}} \\ &= \frac{2}{\sqrt{4}} \\ &= \frac{2}{2} \\ &= 1 \\ \end{align*}$
maka jika dikalikan 100 %, maka $r^2=100$% yang memiliki makna bahwa pengaruh variabel bebas terhadap variabel terikatnya adalah 100 %, sehingga jika ditanyakan pengaruh variabel lainnya akan diperoleh dengan cara 100 % di kurangi dengan hasil $r$, sehingga diperoleh pengaruh variabel lainnya adalah $(100-100)$% = 0 %
Tidak ada komentar:
Posting Komentar