Relasi dan fungsi merupakan dua buah istilah dalam matematika yang saling berhubungan, secara sederhana bisa dikatakan semua relasi adalah fungsi, namun tidak semua fungsi adalah relasi. Untuk lebih jelasnya, silahkan simak pengertian relasi dan fungsi berikut ini.
Definisi Relasi dan Fungsi
Sesuai definisi diatas maka maka secara sederhana jika relasai/fungsi disajikan dalam bentuk diagram panah akan diperoleh sebagai berikut.
- Relasi adalah suatu aturan yang menghubungkan daerah asal $($ Domain $)$ dan daerah hasil $($ kodomain $)$
- Fungsi adalah Suatu relasi yang unik dimana semua anggota domain habis dan mempunyai 1 pasangan di kodomain
Jika susah dalam memahami penjelasan diatas, berikut disediakan video pembahasan singkatnya.
Apabila diperhatikan lebih seksama ada perbedaan jumlah pasangan pada gambar 1 dan gambar 2, terlihat pada gambar 1 semua anggota hanya memiliki 1 pasangan di daerah kodomain, sehingga ini bisa dikatakan suatu relasi dan fungsi. Sedangkan pada gambar 2 ada 1 anggota domain yaitu didi memiliki 2 pasangan di daerah kodomain, sehingga sesuai definisi gambar 2 merupakan suatu relasi namun bukan suatu fungsi.
Pada dasarnya, untuk melihat perbedaan relasi atau fungsi hanya dilihat dari domainnya saja. Apabila domain habis dan memiliki satu pasangan, maka itu adalah relasi dan fungsi, namun jika domain tidak habis atau ada anggota domain tidak memiliki pasangan maka itu bukan fungsi. Lebih jauh fungsi biasanya diberikan dalam bentuk matematika misalnya jika ada domain fungsi $(1,2,3)$ yang dihubungkan dengan sebuah fungsi $2x-1$ maka rangenya dapat ditemukan dengan cara mengganti nilai $x$ pada fungsi dengan nilai domainnya yaitu.
- untuk domain $x=1$ maka kodomainya adalah $2.1-1=1$
- untuk domain $x=2$ maka kodomainya adalah $2.2-1=3$
- untuk domain $x=3$ maka kodomainya adalah $2.3-1=5$
Nah Untuk lebih memahami perbedaan tentang fungsi dan bukan fungsi, silahkan coba menjawab contoh soal berikut.
Contoh Soal
--- Soal No 1 ---
Perhatikan gambar berikut, manakah dari gambar berikut yang merupakan fungsi, dan mana yang bukan fungsi ... .
untuk melihat fungsi atau bukan, lihat domainnya.
Gambar 1 : Fungsi, karena domain habis dan punya 1 pasangan
Gambar 2 : Fungsi, karena domain habis dan punya 1 pasangan
Gambar 3 : Bukan Fungsi, karena ada aggota domain punya 2 pasangan
Gambar 4 : Bukan Fungsi, karena ada aggota domain punya 2 pasangan
Gambar 5 : Bukan Fungsi, karena ada aggota domain punya 2 pasangan
Gambar 6 : Fungsi, karena domain habis dan punya 1 pasangan
--- Soal No 2 ---
Apabila anggota domain adalah 1,2,3 dan anggota kodomain adalah 2,4,6,8 maka apakah relasi duakali lipat dari A ke B merupakan suatu fungsi ....
ia, karena jika dipasangkan sesuai aturan maka pasangan 1 adalah 2, 2 adalah 4 dan 3 adalah 6. Maka sesuai definisi ini merupakan suatu fungsi, karena domain habis dan punya 1 pasangan.
--- Soal No 3 ---
jika diketahui gambar fungsi sebagai berikut, maka coba pasangkan domain dengan kodomainya sesuai dengan fungsi yang diberikan ....
Untuk menemukan range dari fungsi diatas, kita hanya perlu mengannti nilai $x$ sesuai dengan fungsi yang ada sehingga diperoleh
- untuk domain $x=-2$ maka kodomainya adalah $2.(-2)^2-3= 5$
- untuk domain $x=-1$ maka kodomainya adalah $2.(-1)^2-3=-1$
- untuk domain $x=0$ maka kodomainya adalah $2.(0)^2-3=-3$
- untuk domain $x=0$ maka kodomainya adalah $2.(1)^2-3=-1$
- untuk domain $x=0$ maka kodomainya adalah $2.(3)^2-3=15$
- untuk domain $x=0$ maka kodomainya adalah $2.(5)^2-3=47$
maka gambar fungsinya adalah
--- Soal No 4 ---
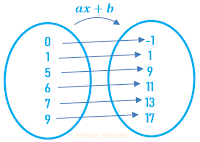
Untuk menemukan nilai $a$ dan $b$ maka cobalah untuk mengganti nilai $x$ dengan domain dan hasilnya sesuai dengan gambar fungsi, kita ambil nilai domainya adalah $0$ dan $1$. untuk $x=0$ diperoleh persamaan
$\begin{align*} ax+b &=-1 \\ a.0+b & = -1 \\ b & =-1 \end{align*}$
untuk nilai $x=1$ maka
$\begin{align*} ax+b &=1 \\ a.1+b & = 1 \\ a+(-1) & = 1 \\ a & = 1+1 \\ a & = 2 \end{align*}$
maka nilai $a+b$ adalah $1+2=3$
NB. jika nilai $x$ menyebabkan adanya persamaan linier dua variabel, maka gunakan konsep eliminasi dan substitusi. Jika lupa klik KLIK INI
$\begin{align*} ax+b &=-1 \\ a.0+b & = -1 \\ b & =-1 \end{align*}$
untuk nilai $x=1$ maka
$\begin{align*} ax+b &=1 \\ a.1+b & = 1 \\ a+(-1) & = 1 \\ a & = 1+1 \\ a & = 2 \end{align*}$
maka nilai $a+b$ adalah $1+2=3$
NB. jika nilai $x$ menyebabkan adanya persamaan linier dua variabel, maka gunakan konsep eliminasi dan substitusi. Jika lupa klik KLIK INI
--- Soal No 5 ---
njika kita perhatikan relasi diatas maka sangat jelas bahwa relasi yang cocok untuk ilustrasi diatas adalah relasi "akar dari", misal kita ambil satu relasi yaitu, 5 adalah akar dari 25
Untuk lebih memahami penjelasan materi diatas Cobalah beberapa soal berikut.
Latihan Soal
| 1 | Coba sebutkan 3 perbedaan mendasar antara relasi dan fungsi yang kamu ketahui |
| 2 | Apakah suatu relasi relasi dapat dikatakan suatu fungsi ? atau apakah suatu fungsi dapat dikatakan suatu relasi ? coba berikan alasanmu! |
| 3 | Cobalah buat suatu relasi kuadrat dari dengan melibatkan 5 anggota ! |
Jika konten ini bermanfaat silahkan share ke teman yang membutuhkan lewat tombol dibawah ini.











Tidak ada komentar:
Posting Komentar