Fungsi Piecewise atau yang kadang disebut sepotong-sepotong merupakan fungsi yang didefinisikan dengan beberapa formula pada beberapa daerah asal. Pada pembahasan kali ini akan dibahas mengenai dua jenis Grafik Fungsinya yaitu fungsi tangga dan fungsi nilai mutlak. Secara umum untuk menggambar fungsi mutlak kita perlu merubah fungsi mutlak menjadi fungsi tangga sesuai definisinya. Namun jika dari gambar grafik kita diminta untuk menemukan apa fungsi tangganya bisa dilakukan dengan menemukan persamaan grafik di batas-batar tertentu dengan rumus $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$ dengan $(x_1,y_1)$ dan $(x_2,y_2)$ adalah titik yang dilalui grafiknya. Untuk lebih jelasnya perhatikan langkah-langkah berikut!
Untuk memahami lebih jauh mengenai barisan dan deret Geometri, berikut disajikan beberapa contoh soal yang dapat digunakan sebagai latihan agar lebih paham mengenai materi barisan dan deret Geometri.
--- Soal No 1 ---
Cobalah gambar Grafik fungsi berikut .
$g(x)=\left\{\begin{matrix}2x+3,x\geq 2 \\ x+5 ,x< 2\end{matrix}\right.$
perhatikan batas nilai pada nilai fungsinya yaitu $2$, maka ambilah beberapa buah titik sebelum dan sesudah nilai fungsi serta nilai fungsinya, sehingga akan diperoleh beberapa titik. Misal akan diambil nilai $x=0,2,3$ maka substitusi nilai $x$ sesuai batas nilainya yaitu.
Untuk $x=0$, maka fungsi yang digunakan adalah $x+5$ sehingga
$ \begin{align*} y &=x+5 \\ y &=0+5 \\ y &=5 \\ \end{align*} $
Untuk $x=2$, maka fungsi yang digunakan adalah $2x+3$ sehingga
$ \begin{align*} y &=2x+3 \\ y &=2.2+3 \\ y &=7 \\ \end{align*} $
Untuk $x=3$, maka fungsi yang digunakan adalah $2x+3$ sehingga
$ \begin{align*} y &=2.3+3 \\ y &=6+3 \\ y &=9 \\ \end{align*} $
dari langkah diatas akan diperoleh titik-titiknya yaitu $A(0,5), B(2,7)$ dan $C(3,9)$ sehingga gambarnya akan diperoleh sebagai berikut.
Untuk $x=0$, maka fungsi yang digunakan adalah $x+5$ sehingga
$ \begin{align*} y &=x+5 \\ y &=0+5 \\ y &=5 \\ \end{align*} $
Untuk $x=2$, maka fungsi yang digunakan adalah $2x+3$ sehingga
$ \begin{align*} y &=2x+3 \\ y &=2.2+3 \\ y &=7 \\ \end{align*} $
Untuk $x=3$, maka fungsi yang digunakan adalah $2x+3$ sehingga
$ \begin{align*} y &=2.3+3 \\ y &=6+3 \\ y &=9 \\ \end{align*} $
dari langkah diatas akan diperoleh titik-titiknya yaitu $A(0,5), B(2,7)$ dan $C(3,9)$ sehingga gambarnya akan diperoleh sebagai berikut.
--- Soal No 2 ---
Cobalah gambar Grafik fungsi berikut .
$g(x)=\left\{\begin{matrix}6-x,x < 2 \\ x+2 , 2 \leq x < 5 \\ 2x-3 ,x \geq 5 \end{matrix}\right.$
Karena pada fungsi terdapat dua buah nilai batas, maka ambil titik uji diantara $2$ dan $5$, Misal akan diambil nilai $x=0,2,3,5,6$ maka substitusi titik tersebut ke persamaan yang memenuhi di soal sehingga diperoleh.
Untuk $x=0$ maka fungsi yang memenuhi adalah $6-x$
$ \begin{align*} y&=6-x \\ &=6-0 \\ &=6 \\ \end{align*} $
Untuk $x=2$ maka fungsi yang memenuhi adalah $x+2$
$ \begin{align*} y&=x+2 \\ &=2+2 \\ &= 4 \\ \end{align*} $
Untuk $x=3$ maka fungsi yang memenuhi adalah $x+2$ dan untuk $x=5$ fungsi yang memenuhi adalah $2x-3$, maka substitusi nilainya sehingga diperoleh nilai $y$ masing-masing $5$ dan $7$.
Untuk $x=6$ maka fungsi yang memenuhi adalah $2x-3$
$ \begin{align*} y&=2x-3 \\ &=2.6-3 \\ &= 9 \\ \end{align*} $
maka dari langkah diatas akan diperoleh beberapa titik yaitu $A(0,6), B(2,4), C(3,5), D(5,7)$ dan $E(6,9)$ sehingga gambar grafiknya adalah sebagai berikut.
Untuk $x=0$ maka fungsi yang memenuhi adalah $6-x$
$ \begin{align*} y&=6-x \\ &=6-0 \\ &=6 \\ \end{align*} $
Untuk $x=2$ maka fungsi yang memenuhi adalah $x+2$
$ \begin{align*} y&=x+2 \\ &=2+2 \\ &= 4 \\ \end{align*} $
Untuk $x=3$ maka fungsi yang memenuhi adalah $x+2$ dan untuk $x=5$ fungsi yang memenuhi adalah $2x-3$, maka substitusi nilainya sehingga diperoleh nilai $y$ masing-masing $5$ dan $7$.
Untuk $x=6$ maka fungsi yang memenuhi adalah $2x-3$
$ \begin{align*} y&=2x-3 \\ &=2.6-3 \\ &= 9 \\ \end{align*} $
maka dari langkah diatas akan diperoleh beberapa titik yaitu $A(0,6), B(2,4), C(3,5), D(5,7)$ dan $E(6,9)$ sehingga gambar grafiknya adalah sebagai berikut.
--- Soal No 3 ---
Cobalah gambar Grafik fungsi $f(x) = | x -2|$
Definisikan terlebih dahulu nilai mutlaknya dengan cara menemukan pembuat nol dalam mutlaknya yaitu.
$ \begin{align*} x-2&=0 \\ x&=2 \\ \end{align*} $
maka sesuai definisi mutlak bentuk $f(x) = | x -2|$ dapat diubah menjadi fungsi tangga menjadi
$f(x)=\left\{\begin{matrix} (x-2),x\geq 2\\-(x-2),x < 2\end{matrix}\right.$
Sehingga cara menggambar grafiknya bisa dilakukan dengan cara mengambil beberapa titik diantara pembuat nolnya yaitu $x=0,2,3$ kemudian substitusi ke soal dan akan diperoleh nilai titiknya adalah $A(0,2), B(2,0)$ dan $C(3,1)$, maka gambarnya adalah sebagai berikut.
$ \begin{align*} x-2&=0 \\ x&=2 \\ \end{align*} $
maka sesuai definisi mutlak bentuk $f(x) = | x -2|$ dapat diubah menjadi fungsi tangga menjadi
$f(x)=\left\{\begin{matrix} (x-2),x\geq 2\\-(x-2),x < 2\end{matrix}\right.$
Sehingga cara menggambar grafiknya bisa dilakukan dengan cara mengambil beberapa titik diantara pembuat nolnya yaitu $x=0,2,3$ kemudian substitusi ke soal dan akan diperoleh nilai titiknya adalah $A(0,2), B(2,0)$ dan $C(3,1)$, maka gambarnya adalah sebagai berikut.
--- Soal No 4 ---
Cobalah gambar Grafik fungsi $f(x)=|2x-6|$
Definisikan terlebih dahulu nilai mutlaknya dengan cara menemukan pembuat nol dalam mutlaknya yaitu.
$ \begin{align*} 2x-6&=0 \\ 2x&=6 \\ x&=\frac{6}{2} \\ x&=3 \\ \end{align*} $
maka sesuai definisi mutlak bentuk $f(x) = | x -2|$ dapat diubah menjadi fungsi tangga menjadi
$f(x)=\left\{\begin{matrix} (2x-6),x\geq 3\\-(2x-6),x < 3\end{matrix}\right.$
Sehingga cara menggambar grafiknya bisa dilakukan dengan cara mengambil beberapa titik diantara pembuat nolnya yaitu $x=0,3,4$ kemudian substitusi ke soal dan akan diperoleh nilai titiknya adalah $A(0,6), B(3,0)$ dan $C(4,2)$, maka gambarnya adalah sebagai berikut.
$ \begin{align*} 2x-6&=0 \\ 2x&=6 \\ x&=\frac{6}{2} \\ x&=3 \\ \end{align*} $
maka sesuai definisi mutlak bentuk $f(x) = | x -2|$ dapat diubah menjadi fungsi tangga menjadi
$f(x)=\left\{\begin{matrix} (2x-6),x\geq 3\\-(2x-6),x < 3\end{matrix}\right.$
Sehingga cara menggambar grafiknya bisa dilakukan dengan cara mengambil beberapa titik diantara pembuat nolnya yaitu $x=0,3,4$ kemudian substitusi ke soal dan akan diperoleh nilai titiknya adalah $A(0,6), B(3,0)$ dan $C(4,2)$, maka gambarnya adalah sebagai berikut.
--- Soal No 5 ---
Cobalah temukan persamaan grafik berikut, kemudian sajikan dalam fungsi mutlak dan fungsi tangga
Sebelum menemukan persamaan fungsi tangganya ingat dulu cara membuat persamaan garis lurus yang melalui sebuah titik $(x_1,y_1)$ dan titik $(x_2,y_2)$ dimana persamaannya dapat ditemukan dengan cara $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$.
Kemudian perhatikan grafik mengalami perubahan gradien atau kemiringan di titik $(-2,0)$ maka jelas sekali bahwa $x=-2$ adalah Pembatas nilai fungsi. Jika sudah ditentukan maka ambil dua buah titik di kanan dan kiri fungsi kemudian temukan persamaan garisnya.
Untuk titik yang berada di sebalah kiri $x=-2$ akan diambil titik $(-4,2)$ dan $(-3,1)$
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-4)}{-3-(-4)} &= \frac{y-2}{1-2}\\ \frac{x+4}{1)} &= \frac{y-2}{-1}\\ -1.(x+4) &= (y-2).1\\ -x-y &= 2 \\ x + y &= -2 \\ y &= -2-x \\ \end{align*} $
Untuk titik yang berada di sebalah kanan $x=-2$ akan diambil titik $(-1,1)$ dan $(0,2)$
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-1)}{0-(-1)} &= \frac{y-1}{2-1}\\ \frac{x+1}{1)} &= \frac{y-1}{1}\\ (x+1) &= (y-1)\\ x-y &= -2 \\ y &= x+2 \\ \end{align*} $
sehingga melalui kedua persamaan garis diatas akan diperoleh persamaan fungsi tangga sebagai berikut.
$ f(x)=\left\{\begin{matrix} x+2,x\geq 2\\-x-2,x < 2\end{matrix}\right.$
Kemudian perhatikan grafik mengalami perubahan gradien atau kemiringan di titik $(-2,0)$ maka jelas sekali bahwa $x=-2$ adalah Pembatas nilai fungsi. Jika sudah ditentukan maka ambil dua buah titik di kanan dan kiri fungsi kemudian temukan persamaan garisnya.
Untuk titik yang berada di sebalah kiri $x=-2$ akan diambil titik $(-4,2)$ dan $(-3,1)$
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-4)}{-3-(-4)} &= \frac{y-2}{1-2}\\ \frac{x+4}{1)} &= \frac{y-2}{-1}\\ -1.(x+4) &= (y-2).1\\ -x-y &= 2 \\ x + y &= -2 \\ y &= -2-x \\ \end{align*} $
Untuk titik yang berada di sebalah kanan $x=-2$ akan diambil titik $(-1,1)$ dan $(0,2)$
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-1)}{0-(-1)} &= \frac{y-1}{2-1}\\ \frac{x+1}{1)} &= \frac{y-1}{1}\\ (x+1) &= (y-1)\\ x-y &= -2 \\ y &= x+2 \\ \end{align*} $
sehingga melalui kedua persamaan garis diatas akan diperoleh persamaan fungsi tangga sebagai berikut.
$ f(x)=\left\{\begin{matrix} x+2,x\geq 2\\-x-2,x < 2\end{matrix}\right.$
--- Soal No 6 ---
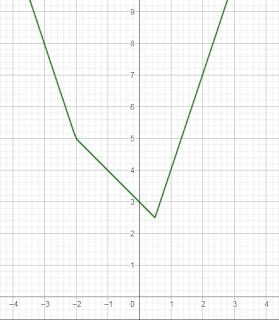
Cobalah temukan persamaan grafik berikut, kemudian sajikan dalam fungsi fungsi tangga
Sebelum menemukan persamaan fungsi tangganya ingat dulu cara membuat persamaan garis lurus yang melalui sebuah titik $(x_1,y_1)$ dan titik $(x_2,y_2)$ dimana persamaannya dapat ditemukan dengan cara $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$
Kemudian perhatikan grafik mengalami perubahan gradien atau kemiringan di titik $(-2,0)$ dan $(\frac{1}{2},\frac{3}{2})$ maka jelas sekali bahwa $x=-2$ dan $x=\frac{1}{2}$ adalah Pembatas nilai fungsi. Jika sudah ditentukan maka ambil dua buah titik di kanan dan kiri fungsi kemudian temukan persamaan garisnya.
untuk $x < 2$ ambil dua buah titik yaitu titik $(-2,5)$ dan $(-3,8)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-2)}{-3-(-2)} &= \frac{y-5}{8-5}\\ \frac{x+2}{-1)} &= \frac{y-5}{3}\\ 3x+6 &= -y+5\\ y &= -3x-1 \\ \end{align*} $
untuk $2 \leq x < \frac{1}{2}$ ambil dua buah titik yaitu titik $(-1,4)$ dan $(0,3)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-1)}{0-(-1)} &= \frac{y-4}{3-4}\\ \frac{x+1}{1)} &= \frac{y-4}{-1}\\ -x-1 &= y-4\\ y &= -x+3 \\ \end{align*} $
untuk $x \geq \frac{1}{2}$ ambil dua buah titik yaitu titik $(1,4)$ dan $(2,7)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-1}{2-1)} &= \frac{y-4}{7-4}\\ \frac{x-1}{1)} &= \frac{y-4}{3}\\ 3x-3 &= y-4\\ y &= 3x+1 \\ \end{align*} $
Sehingga dari persamaan yang dieperoleh diatas, maka fungsi tangganya dapat dibuat seperti berikut ini.
$\left\{\begin{matrix} -3x-1, x < -2\\ -x+3, -2 \leq x <\frac{1}{2} \\ 3x+1, x /geq \frac{1}{2} \\ \end{matrix}\right.$
Kemudian perhatikan grafik mengalami perubahan gradien atau kemiringan di titik $(-2,0)$ dan $(\frac{1}{2},\frac{3}{2})$ maka jelas sekali bahwa $x=-2$ dan $x=\frac{1}{2}$ adalah Pembatas nilai fungsi. Jika sudah ditentukan maka ambil dua buah titik di kanan dan kiri fungsi kemudian temukan persamaan garisnya.
untuk $x < 2$ ambil dua buah titik yaitu titik $(-2,5)$ dan $(-3,8)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-2)}{-3-(-2)} &= \frac{y-5}{8-5}\\ \frac{x+2}{-1)} &= \frac{y-5}{3}\\ 3x+6 &= -y+5\\ y &= -3x-1 \\ \end{align*} $
untuk $2 \leq x < \frac{1}{2}$ ambil dua buah titik yaitu titik $(-1,4)$ dan $(0,3)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-(-1)}{0-(-1)} &= \frac{y-4}{3-4}\\ \frac{x+1}{1)} &= \frac{y-4}{-1}\\ -x-1 &= y-4\\ y &= -x+3 \\ \end{align*} $
untuk $x \geq \frac{1}{2}$ ambil dua buah titik yaitu titik $(1,4)$ dan $(2,7)$, sehingga persamaanya adalah
$ \begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{y-y_1}{y_2-y_1}\\ \frac{x-1}{2-1)} &= \frac{y-4}{7-4}\\ \frac{x-1}{1)} &= \frac{y-4}{3}\\ 3x-3 &= y-4\\ y &= 3x+1 \\ \end{align*} $
Sehingga dari persamaan yang dieperoleh diatas, maka fungsi tangganya dapat dibuat seperti berikut ini.
$\left\{\begin{matrix} -3x-1, x < -2\\ -x+3, -2 \leq x <\frac{1}{2} \\ 3x+1, x /geq \frac{1}{2} \\ \end{matrix}\right.$











Tidak ada komentar:
Posting Komentar