Pada pembelajaran kali ini akan dibahas mengenai grafik fungsi Eksponen, mirip dengan fungsi logaritma fungsi eksponen akan selalu mengalami kenaikan atau penurunan tergantung dari nilai-nilai yang ada di dalam grafiknya. Banyak permasalahan yang dapat dimodelkan dengan menggunakan konsep grafik eksponensial. tentunya permaslahan yang selalu mengalami penurunan dan kenaikan tertentu. oleh sebab itu sangatlah penting untuk mengetahui bentuk dan bagaimana cara menggambar grafik fungsi eksponen
Untuk lebih memahami grafik fungsi eksponen, silahkan simak penjelasan berikut ini.
Untuk lebih memperdalam pemahamam mengenai materi diatas, berikut disajikan beberapa contoh dan latihan soal yang bisa dicoba. Silahkan coba sediri terlebih dulu setiap permasalahan yang diberikan sebelum melihat dan memahami pembahasanya. Sehingga jika sudah memahaminya bisa mengerjakan latihan soal secara mandiri.
Contoh Soal
Soal No 1
cobalah gambar grafik fungsi $f(x)=3^x$ ...
Untuk menggambar grafik fungsinya, ambilah niali x yang membuat kita mudah dalam menghitung, misalnya akan diambik nilai $x$ adalah $1$ dan $2$, maka diperoleh
untuk nilai $x=1$ maka
$\begin{align*} f(x) &= 3^x \\ &= 3^1\\ &= 3\\ \end{align*}$
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 3^2 \\ &= 3^2\\ &= 9\\ \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(1,3)$ dan $(2,9)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
untuk nilai $x=1$ maka
$\begin{align*} f(x) &= 3^x \\ &= 3^1\\ &= 3\\ \end{align*}$
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 3^2 \\ &= 3^2\\ &= 9\\ \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(1,3)$ dan $(2,9)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
Soal No 2
cobalah gambar grafik fungsi $f(x)=3^{x-1}$ ...
Untuk menggambar grafik fungsinya, ambilah niali x yang membuat kita mudah dalam menghitung, misalnya akan diambik nilai $x$ adalah $1$ dan $2$, maka diperoleh
untuk nilai $x=1$ maka
$\begin{align*} f(x) &= 3^{x-1} \\ &= 3^{1-1} \\ &= 3^0 \\ &= 1 \end{align*}$
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 3^{x-1} \\ &= 3^{2-1}\\ &= 3^1\\ &= 3 \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(1,1)$ dan $(2,3)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
untuk nilai $x=1$ maka
$\begin{align*} f(x) &= 3^{x-1} \\ &= 3^{1-1} \\ &= 3^0 \\ &= 1 \end{align*}$
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 3^{x-1} \\ &= 3^{2-1}\\ &= 3^1\\ &= 3 \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(1,1)$ dan $(2,3)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
Soal No 3
cobalah gambar grafik fungsi $f(x)=4.3^{x-2}$ ...
Untuk menggambar grafik fungsinya, ambilah niali x yang membuat kita mudah dalam menghitung, misalnya akan diambik nilai $x$ adalah $2$ dan $3$, maka diperoleh
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 4.3^{x-2} \\ &= 4.3^{2-2} \\ &= 4.3^0 \\ &= 4 \end{align*}$
untuk nilai $x=3$ maka
$\begin{align*} f(x) &= 4.3^{3-2}\\ &= 4.3^{3-2}\\ &= 4.3^1\\ &= 12 \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(2,4)$ dan $(3,12)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
untuk nilai $x=2$ maka
$\begin{align*} f(x) &= 4.3^{x-2} \\ &= 4.3^{2-2} \\ &= 4.3^0 \\ &= 4 \end{align*}$
untuk nilai $x=3$ maka
$\begin{align*} f(x) &= 4.3^{3-2}\\ &= 4.3^{3-2}\\ &= 4.3^1\\ &= 12 \end{align*}$
maka melalui langkah diatas, akan diperoleh dua buah titik $(2,4)$ dan $(3,12)$. dan perhatikan juga berapapun nilai x yang dimasukan maka tidak akan pernah sama dengan nol, sehingga grafik tidak akan pernah memotong sumbu $x$ dan akan bernilai mendekati nol jika diambil nilai $x$ minus tah hingga. Sehingga gambarnya adalah sebagai berikut.
Soal No 4
Perhatikan Grafik Fungsi eksponen berikut ini !
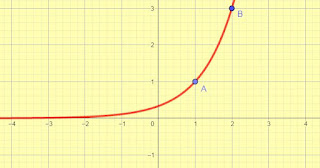
Temukan persamaan yang memuat grafik diatas
Sebelum menemukan grafik fungsi dari gambar diatas, maka akan dimisalkan dulu persamaan grafiknya adalah $y=a.b^x$, kemudian ambil dua buah titik yang melalui kurva. Dalam hal ini akan diambil titik $(0,1)$ dan $(1,5)$ kemudian substitusi titik ke persamaan yang sudah dimisalkan sehingga.
Untuk titik $(0,1)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 1 &= a.b^0\\ a &= 1 \end{align*}$
Untuk titik $(1,5)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ 5 &= a.b^1\\ 5 &= a.b\\ 5 &= 1.b \\ b &= 5 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah $f(x)=1.5^x=5^x$
Untuk titik $(0,1)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 1 &= a.b^0\\ a &= 1 \end{align*}$
Untuk titik $(1,5)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ 5 &= a.b^1\\ 5 &= a.b\\ 5 &= 1.b \\ b &= 5 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah $f(x)=1.5^x=5^x$
Soal No 5
Perhatikan Grafik Fungsi eksponen berikut ini !
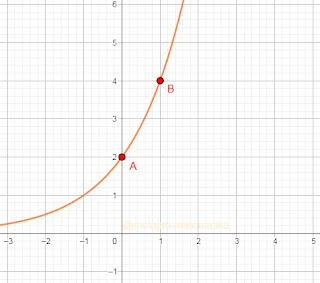
Temukan persamaan yang memuat grafik diatas
Sebelum menemukan grafik fungsi dari gambar diatas, maka akan dimisalkan dulu persamaan grafiknya adalah $y=a.b^x$, kemudian ambil dua buah titik yang melalui kurva. Dalam hal ini akan diambil titik $(0,2)$ dan $(1,4)$ kemudian substitusi titik ke persamaan yang sudah dimisalkan sehingga.
Untuk titik $(0,2)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 2 &= a.b^0\\ a &= 2 \end{align*}$
Untuk titik $(1,4)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 4 &= a.b^1\\ 4 &= a.b\\ 4 &= 2.b \\ b &= 2 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah
$\begin{align*} f(x) &= a.b^x\\ &= 2.2^x\\ &= 2^1.2^x\\ &= 2^{1+x}\\ \end{align*}$
Untuk titik $(0,2)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 2 &= a.b^0\\ a &= 2 \end{align*}$
Untuk titik $(1,4)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ 4 &= a.b^1\\ 4 &= a.b\\ 4 &= 2.b \\ b &= 2 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah
$\begin{align*} f(x) &= a.b^x\\ &= 2.2^x\\ &= 2^1.2^x\\ &= 2^{1+x}\\ \end{align*}$
Soal No 6
Perhatikan Grafik Fungsi eksponen berikut ini !
Temukan persamaan yang memuat grafik diatas
Sebelum menemukan grafik fungsi dari gambar diatas, maka akan dimisalkan dulu persamaan grafiknya adalah $y=a.b^x$, kemudian ambil dua buah titik yang melalui kurva. Dalam hal ini akan diambil titik $(0,-4)$ dan $(2,-16)$ kemudian substitusi titik ke persamaan yang sudah dimisalkan sehingga.
Untuk titik $(0,-4)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ -4 &= a.b^0\\ a &= -4 \end{align*}$
Untuk titik $(2,-16)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ -16 &= a.b^2\\ -16 &= -4.b^2\\ 4 &= b^2 \\ b &= 2 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah
$\begin{align*} f(x) &= a.b^x\\ &= -4.2^x\\ &= -2^2.2^x\\ &= 2^{2+x}\\ \end{align*}$
Untuk titik $(0,-4)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ -4 &= a.b^0\\ a &= -4 \end{align*}$
Untuk titik $(2,-16)$ diperoleh
$\begin{align*} f(x) &= a.b^x\\ y &= a.b^x\\ -16 &= a.b^2\\ -16 &= -4.b^2\\ 4 &= b^2 \\ b &= 2 \\ \end{align*}$
maka grafik fungsi dari gambar diatas adalah
$\begin{align*} f(x) &= a.b^x\\ &= -4.2^x\\ &= -2^2.2^x\\ &= 2^{2+x}\\ \end{align*}$
Tidak ada komentar:
Posting Komentar