Berikut ini disajikan latihan soal yang sekaligus dapat digunakan sebagai kisi-kisi dalam persiapan menempuh Penilaian Akhir Semester atau PAS. Silahkan dipelajari dan disimak dengan baik.
--- Soal No 1 ---
NIlai dari $\left ( \frac{3}{2a} \right )^{-2}$ adalah ... .
A. $-\frac{9}{4a^2}$
B. $-\frac{6}{2a^2}$
C. $-\frac{3}{a^2}$
D. $\frac{4a^2}{9}$
E. $\frac{2a^2}{3}$
A. $-\frac{9}{4a^2}$
B. $-\frac{6}{2a^2}$
C. $-\frac{3}{a^2}$
D. $\frac{4a^2}{9}$
E. $\frac{2a^2}{3}$
Kunci : D. $\frac{4a^2}{9}$
Dengan menggunakan sifat-sifat bilangan berpangkat maka diperoleh.
$\begin{align*} \left ( \frac{3}{2a} \right )^{-2} &= \left ( \frac{3^{-2}}{(2a)^{-2}} \right ) \\ &= \frac{(2a)^{2}}{3^{2}} \\ &= \frac{4a^{2}}{9} \\ \end{align*}$
Jadi jawaban yang paling tepat adalah $\frac{4a^2}{9}$
Dengan menggunakan sifat-sifat bilangan berpangkat maka diperoleh.
$\begin{align*} \left ( \frac{3}{2a} \right )^{-2} &= \left ( \frac{3^{-2}}{(2a)^{-2}} \right ) \\ &= \frac{(2a)^{2}}{3^{2}} \\ &= \frac{4a^{2}}{9} \\ \end{align*}$
Jadi jawaban yang paling tepat adalah $\frac{4a^2}{9}$
--- Soal No 2 ---
Jika diketahui nilai dari $x=\frac{1}{3},y=\frac{1}{5}$ dan $z=2$ maka nilai dari $\frac{x^{-4}yz^{-2}}{x^{-3}y^{2}z^{-4}}$... .
A. 32
B. 64
C. 60
D. 100
E. 34
A. 32
B. 64
C. 60
D. 100
E. 34
Kunci : C. 60
Dengan sifat bilangan berpangkat sederhanakan bentuk dalam soal, sehingga menjadi
$\begin{align*} \frac{x^{-4}yz^{-2}}{x^{-3}y^{2}z^{-4}} &= \frac{z^{-2-(-4)}}{x^{-3-(-4)}y^{2-1}} \\ &= \frac{z^{2}}{x^{1}y^{1}} \\ &= \frac{z^{2}}{xy} \\ \end{align*}$
kemudian ganti nilai $x,y$ dan $z$ dengan nilai yang diketahui yaitu $x=\frac{1}{3},y=\frac{1}{5}$ dan $z=2$ sehingga
$\begin{align*} &= \frac{z^{2}}{xy} \\ &= \frac{2^{2}}{\frac{1}{3}.\frac{1}{5}} \\ &= \frac{4}{\frac{1}{15}} \\ &= 4.\frac{15}{1} \\ &= 60 \end{align*}$
maka jawaban yang paling tepat adalah $C. 60$
Dengan sifat bilangan berpangkat sederhanakan bentuk dalam soal, sehingga menjadi
$\begin{align*} \frac{x^{-4}yz^{-2}}{x^{-3}y^{2}z^{-4}} &= \frac{z^{-2-(-4)}}{x^{-3-(-4)}y^{2-1}} \\ &= \frac{z^{2}}{x^{1}y^{1}} \\ &= \frac{z^{2}}{xy} \\ \end{align*}$
kemudian ganti nilai $x,y$ dan $z$ dengan nilai yang diketahui yaitu $x=\frac{1}{3},y=\frac{1}{5}$ dan $z=2$ sehingga
$\begin{align*} &= \frac{z^{2}}{xy} \\ &= \frac{2^{2}}{\frac{1}{3}.\frac{1}{5}} \\ &= \frac{4}{\frac{1}{15}} \\ &= 4.\frac{15}{1} \\ &= 60 \end{align*}$
maka jawaban yang paling tepat adalah $C. 60$
--- Soal No 3 ---
Hasil Operasi dari $3\sqrt{50}-\sqrt{8}+\sqrt{128}-5\sqrt{18}$... .
A. $6\sqrt{2}$
B. $4\sqrt{2}$
C. $-6\sqrt{2}$
D. $-4\sqrt{2}$
E. $5\sqrt{2}$
A. $6\sqrt{2}$
B. $4\sqrt{2}$
C. $-6\sqrt{2}$
D. $-4\sqrt{2}$
E. $5\sqrt{2}$
Kunci : A. $6\sqrt{2}$
Dengan sifat bilangan akan samakan bilangan yang ada di dalam akar dengan cara
$\begin{align*} &= 3\sqrt{50}-\sqrt{8}+\sqrt{128}-5\sqrt{18} \\ &= 3\sqrt{25.2}-\sqrt{4.2}+\sqrt{64.2}-5\sqrt{9.2} \\ &= 3.5\sqrt{2}-2\sqrt{2}+8\sqrt{2}-5.3\sqrt{2} \\ &= 15\sqrt{2}-2\sqrt{2}+8\sqrt{2}-15\sqrt{2} \\ &= 6\sqrt{2} \end{align*}$
maka jawaban yang paling tepat adalah A. $6\sqrt{2}$
Dengan sifat bilangan akan samakan bilangan yang ada di dalam akar dengan cara
$\begin{align*} &= 3\sqrt{50}-\sqrt{8}+\sqrt{128}-5\sqrt{18} \\ &= 3\sqrt{25.2}-\sqrt{4.2}+\sqrt{64.2}-5\sqrt{9.2} \\ &= 3.5\sqrt{2}-2\sqrt{2}+8\sqrt{2}-5.3\sqrt{2} \\ &= 15\sqrt{2}-2\sqrt{2}+8\sqrt{2}-15\sqrt{2} \\ &= 6\sqrt{2} \end{align*}$
maka jawaban yang paling tepat adalah A. $6\sqrt{2}$
--- Soal No 4 ---
Bentuk sederhana dari $\frac{6(3+\sqrt{5})(3-\sqrt{5})}{2+\sqrt{6}}$... .
A. $24+12\sqrt{6}$
B. $-24+12\sqrt{6}$
C. $24-12\sqrt{6}$
D. $-24-12\sqrt{6}$
E. $24+\sqrt{6}$
A. $24+12\sqrt{6}$
B. $-24+12\sqrt{6}$
C. $24-12\sqrt{6}$
D. $-24-12\sqrt{6}$
E. $24+\sqrt{6}$
Kunci : B. $-24+12\sqrt{6}$
Jika dilihat dari soal, maka kalian dulu bentuk yang ada di pembilang kemudian kalikan dengan kawan dari penyebutnya. Yaitu
$\begin{align*} \frac{6(3+\sqrt{5})(3-\sqrt{5}}{2+\sqrt{6}} &= \frac{6(9-5)}{2+\sqrt{6}} \\ &= \frac{24}{2+\sqrt{6}}.\frac{2-\sqrt{6}}{2-\sqrt{6}} \\ &= \frac{24(2-\sqrt{6})}{4-6} \\ &= \frac{24(2-\sqrt{6})}{-2} \\ &= -12(2-\sqrt{6}) \\ &= -24+12\sqrt{6} \end{align*}$
maka jawaban yang paling tepat adalah B. $-24+12\sqrt{6}$
Jika dilihat dari soal, maka kalian dulu bentuk yang ada di pembilang kemudian kalikan dengan kawan dari penyebutnya. Yaitu
$\begin{align*} \frac{6(3+\sqrt{5})(3-\sqrt{5}}{2+\sqrt{6}} &= \frac{6(9-5)}{2+\sqrt{6}} \\ &= \frac{24}{2+\sqrt{6}}.\frac{2-\sqrt{6}}{2-\sqrt{6}} \\ &= \frac{24(2-\sqrt{6})}{4-6} \\ &= \frac{24(2-\sqrt{6})}{-2} \\ &= -12(2-\sqrt{6}) \\ &= -24+12\sqrt{6} \end{align*}$
maka jawaban yang paling tepat adalah B. $-24+12\sqrt{6}$
--- Soal No 5 ---
Diketahui $^3log5=a$ dan $^2log3=b$ maka berapakah nilai dari $^6 log 10$... .
A. $\frac{ab+1}{ab}$
B. $\frac{a+1}{b+1}$
C. $\frac{ab+1}{1+ab}$
D. $\frac{ab+1}{b+1}$
E. $\frac{b+1}{ab+1}$
A. $\frac{ab+1}{ab}$
B. $\frac{a+1}{b+1}$
C. $\frac{ab+1}{1+ab}$
D. $\frac{ab+1}{b+1}$
E. $\frac{b+1}{ab+1}$
Kunci : D. $\frac{ab+1}{b+1}$
Ingatlah kembali sifat-sifat logaritma, sehingga bentuk soal bisa diubah menjadi
$\begin{align*} ^6 log 10 &= \frac{^plog 10}{^plog6} \\ &= \frac{^plog(2.5) }{^plog(2.3)} \\ \end{align*}$
Agar nilai logaritma ada, maka nilai $p$ diganti dengan $3$ karena nilainya ada dikedua bentuk log yang diketahui, sehingga
$\begin{align*} ^6 log 10 &= \frac{^plog 10}{^plog6} \\ &= \frac{^plog(2.5) }{^plog(2.3)} \\ &= \frac{^3log2+^3log5 }{^3log2+^3log3} \\ &= \frac{\frac{1}{b}+a}{\frac{1}{b}+1} \\ &= \frac{\frac{1+ab}{b} }{\frac{1+b}{b}} \\ &= \frac{1+ab}{1+b} \end{align*}$
maka jawaban yang paling tepat adalah D. $\frac{ab+1}{b+1}$
Ingatlah kembali sifat-sifat logaritma, sehingga bentuk soal bisa diubah menjadi
$\begin{align*} ^6 log 10 &= \frac{^plog 10}{^plog6} \\ &= \frac{^plog(2.5) }{^plog(2.3)} \\ \end{align*}$
Agar nilai logaritma ada, maka nilai $p$ diganti dengan $3$ karena nilainya ada dikedua bentuk log yang diketahui, sehingga
$\begin{align*} ^6 log 10 &= \frac{^plog 10}{^plog6} \\ &= \frac{^plog(2.5) }{^plog(2.3)} \\ &= \frac{^3log2+^3log5 }{^3log2+^3log3} \\ &= \frac{\frac{1}{b}+a}{\frac{1}{b}+1} \\ &= \frac{\frac{1+ab}{b} }{\frac{1+b}{b}} \\ &= \frac{1+ab}{1+b} \end{align*}$
maka jawaban yang paling tepat adalah D. $\frac{ab+1}{b+1}$
--- Soal No 6 ---
tentukam hasil dari $ \left ( ab^{2} \right )^{-1}\times \left ( a^{5}b^{8} \right )$ ... .
A. $a^4b^5$
B. $a^6b^6$
C. $a^4b^6$
D. $a^6b^{-6}$
E. $a^4b^{-6}$
A. $a^4b^5$
B. $a^6b^6$
C. $a^4b^6$
D. $a^6b^{-6}$
E. $a^4b^{-6}$
Kunci : C. $a^4b^6$
dengan menggunakan sifat-sifat bilangan berpangkat diperoleh
$\begin{align*} \left ( ab^{2} \right )^{-1}\times \left ( a^{5}b^{8} \right ) &= a^{-1}b^{-2}\times a^{5}b^{8} \\ &= a^{-1+5}b^{-2+8} \\ &= a^{4}b^{6} \\ \end{align*}$
maka jawaban yang paling tepat adalah C. $a^4b^6$
dengan menggunakan sifat-sifat bilangan berpangkat diperoleh
$\begin{align*} \left ( ab^{2} \right )^{-1}\times \left ( a^{5}b^{8} \right ) &= a^{-1}b^{-2}\times a^{5}b^{8} \\ &= a^{-1+5}b^{-2+8} \\ &= a^{4}b^{6} \\ \end{align*}$
maka jawaban yang paling tepat adalah C. $a^4b^6$
--- Soal No 7 ---
Banyak kursi pada barisan pertama disebuah aula adalah 15 sedangkan pada baris ke dua adalah 19 dan seterusmya bertambah empat barisan berikutnya.jika ada 20 baris kursi, maka jumlah kursi dalam auala tersebut adalah ... .
A. 1006
B. 1060
C. 1600
D. 1660
E. 1066
A. 1006
B. 1060
C. 1600
D. 1660
E. 1066
Kunci : B. 1060
Persamalahan diatas dapat diselesaikan dengan menemukan nilai $Sn$ atau jumlah n suku pertama dengan nilai suku awal $a=15$ dengan beda $b=19-15=4$ dengan $n=20$ sehingga
$\begin{align*} Sn &= \frac{n}{2}(2a+(n-1)b) \\ &= \frac{20}{2}(2.15+(20-1)4) \\ &= 10(30+76) \\ &= 10(106) \\ &= 1060 \end{align*}$
maka jawaban yang paling tepat adalah B. 1060
Persamalahan diatas dapat diselesaikan dengan menemukan nilai $Sn$ atau jumlah n suku pertama dengan nilai suku awal $a=15$ dengan beda $b=19-15=4$ dengan $n=20$ sehingga
$\begin{align*} Sn &= \frac{n}{2}(2a+(n-1)b) \\ &= \frac{20}{2}(2.15+(20-1)4) \\ &= 10(30+76) \\ &= 10(106) \\ &= 1060 \end{align*}$
maka jawaban yang paling tepat adalah B. 1060
--- Soal No 8 ---
Diketahui suatu barisan geometri suku ke tiga adalah 4 dan suku ke tujuh adalah 324 suku ke enam barisan geometri tersebut adalah ... .
A. 102
B. 108
C. 120
D. 128
E. 180
A. 102
B. 108
C. 120
D. 128
E. 180
Kunci : B. 108
dari informasi di soal diperoleh.
$\begin{align*} U_3 &= 4 \\ ar^{3-1} &= 4 \\ ar^2 &= 4 \end{align*}$
dan
$\begin{align*} U_7 &= 324 \\ ar^{7-1} &= 324 \\ ar^6 &= 324 \end{align*}$
dari kedua persamaan di atas, maka bisa menggunakan cara substitusi untuk menemukan nilai $r$ yaitu
$\begin{align*} U_7 &= 324 \\ ar^{7-1} &= 324 \\ ar^6 &= 324 \\ ar^2.r^4 &= 324 \\ 4.r^4 &= 324 \\ r^4 &= 81 \\ r &= 3 \end{align*}$
karena nilai $r=3$ maka nilai $a$ diperoleh dengan cara
$\begin{align*} ar^2 &= 4 \\ a3^2 &= 4 \\ a &= \frac{4}{9} \\ \end{align*}$
maka nilai suku ke enemnya adalah. $U_6=ar^{n-1}=\frac{4}{9}.3^5=108$
dari informasi di soal diperoleh.
$\begin{align*} U_3 &= 4 \\ ar^{3-1} &= 4 \\ ar^2 &= 4 \end{align*}$
dan
$\begin{align*} U_7 &= 324 \\ ar^{7-1} &= 324 \\ ar^6 &= 324 \end{align*}$
dari kedua persamaan di atas, maka bisa menggunakan cara substitusi untuk menemukan nilai $r$ yaitu
$\begin{align*} U_7 &= 324 \\ ar^{7-1} &= 324 \\ ar^6 &= 324 \\ ar^2.r^4 &= 324 \\ 4.r^4 &= 324 \\ r^4 &= 81 \\ r &= 3 \end{align*}$
karena nilai $r=3$ maka nilai $a$ diperoleh dengan cara
$\begin{align*} ar^2 &= 4 \\ a3^2 &= 4 \\ a &= \frac{4}{9} \\ \end{align*}$
maka nilai suku ke enemnya adalah. $U_6=ar^{n-1}=\frac{4}{9}.3^5=108$
--- Soal No 9 ---
Suatu modal sebesar Rp. 3.200.000,00 diperbungakan dengan bunga tunggal setelah 10 tahun modal menjadi Rp. 4.000.000,00 berapa persen bunga yang didapat ... .
A. 2,0 %
B. 2,5 %
C. 0,25 %
D. 1,25 %
E. 0,20 %
A. 2,0 %
B. 2,5 %
C. 0,25 %
D. 1,25 %
E. 0,20 %
Kunci : B. 2,5 %
dengan menggunakan rumus bunga tunggal dimana $Mo$=modal $Ma$=modal akhir $n$ lama menabung dan $i$ besar suku bunga bank diperoleh.
$\begin{align*} Ma &= Mo+Mo.n.i \\ 4.000.000 &= 3.200.000+3.200.000.10.i \\ 800.000 &= 3.200.000.10.i \\ \frac{800.000}{3.200.000.10} &= i \\ \frac{1}{40} &= i \\ 2,5 \% &= i \\ \end{align*}$
maka suku bunga bank tersebut adalah $2,5 \%$
dengan menggunakan rumus bunga tunggal dimana $Mo$=modal $Ma$=modal akhir $n$ lama menabung dan $i$ besar suku bunga bank diperoleh.
$\begin{align*} Ma &= Mo+Mo.n.i \\ 4.000.000 &= 3.200.000+3.200.000.10.i \\ 800.000 &= 3.200.000.10.i \\ \frac{800.000}{3.200.000.10} &= i \\ \frac{1}{40} &= i \\ 2,5 \% &= i \\ \end{align*}$
maka suku bunga bank tersebut adalah $2,5 \%$
--- Soal No 10 ---
Pada awal tahun 2023 Bunga Meminjam uang sebesar Rp 5.000.000,00 di bank dengan suku bunga tunggal 1,5% per bulan besar bunga yang harus dibayar Bunga setelah 10 bulan adalah ... .
A. Rp 825.000
B. Rp 750.000
C. Rp 675.000
D. Rp 600.000
E. Rp 525.000
A. Rp 825.000
B. Rp 750.000
C. Rp 675.000
D. Rp 600.000
E. Rp 525.000
Kunci :
Bunga dapat dicari dengan cara mengalikan suku bunga dengan jumlah uang yang dipinjam. Namun dalam soal bunga yang ditanyakan selama 10 bulan maka besar bunganya adalah
$\begin{align*} \text {Bunga} &= Mo.i.n \\ &= 5.000.000.1,5 \%.10 \\ &= 750.000 \\ \end{align*}$
maka besar bunganya adalah $750.000$
Bunga dapat dicari dengan cara mengalikan suku bunga dengan jumlah uang yang dipinjam. Namun dalam soal bunga yang ditanyakan selama 10 bulan maka besar bunganya adalah
$\begin{align*} \text {Bunga} &= Mo.i.n \\ &= 5.000.000.1,5 \%.10 \\ &= 750.000 \\ \end{align*}$
maka besar bunganya adalah $750.000$
--- Soal No 11---
Diketahui rumus ke-n barisan aritmatika adalah $Un=4n-5$ tentukan jumalah 12 suku pertama barisan tersebut... .
A. 170
B. 209
C. 252
D. 299
E. 350
A. 170
B. 209
C. 252
D. 299
E. 350
Kunci : C. 252
Untuk menyelesaikan soal, temukan dulu nilai suku awak dan bedanya dengan cara sebagai berikut.
$\begin{align*} Un &= 4n-5 \\ U_1 &= 4.1-5 \\ &= -1 \\ \end{align*}$
$\begin{align*} Un &= 4n-5 \\ U_2 &= 4.2-5 \\ &= 3 \\ \end{align*}$
maka dari ilustrasi tersebut diperoleh $a=-1$ dan $b=U2-U1=4$, sehingga
$\begin{align*} Sn &= \frac{n}{2}(2.a+(n-1).b) \\ &= \frac{12}{2}(2.(-1)+(12-1).4) \\ &= 6(-2+44) \\ &= 6(42) \\ &= 252 \end{align*}$
maka nilai dari $S_{12} =252$
Untuk menyelesaikan soal, temukan dulu nilai suku awak dan bedanya dengan cara sebagai berikut.
$\begin{align*} Un &= 4n-5 \\ U_1 &= 4.1-5 \\ &= -1 \\ \end{align*}$
$\begin{align*} Un &= 4n-5 \\ U_2 &= 4.2-5 \\ &= 3 \\ \end{align*}$
maka dari ilustrasi tersebut diperoleh $a=-1$ dan $b=U2-U1=4$, sehingga
$\begin{align*} Sn &= \frac{n}{2}(2.a+(n-1).b) \\ &= \frac{12}{2}(2.(-1)+(12-1).4) \\ &= 6(-2+44) \\ &= 6(42) \\ &= 252 \end{align*}$
maka nilai dari $S_{12} =252$
--- Soal No 12 ---
Suku keempat dan suku ketujuh barisan aritmetika berturut-turut adalah 17 dan 29. Suku ke-25 barisan tersebut adalah... .
A. 97
B. 101
C. 105
D. 109
E. 113
A. 97
B. 101
C. 105
D. 109
E. 113
Kunci :
Untuk menemukan nilai bedanya, gunakan informasi $U_4=17$ dan $U_7=29$ maka
$\begin{align*} 7b-4b &= 29-17 \\ 3b &= 12 \\ b &= 4 \\ \end{align*}$
maka nilai a diperleh dengan cara
$\begin{align*} U4 &= 17 \\ a+3b &= 17 \\ a+12 &= 17 \\ a &= 5 \\ \end{align*}$
maka nilai dari $U_25$ adalah
$\begin{align*} U_{25} &= a+24b \\ &= 5+24.4 \\ &= 5 + 96 \\ &= 101 \\ \end{align*}$
maka nilai dari $U_{25}=101$
Untuk menemukan nilai bedanya, gunakan informasi $U_4=17$ dan $U_7=29$ maka
$\begin{align*} 7b-4b &= 29-17 \\ 3b &= 12 \\ b &= 4 \\ \end{align*}$
maka nilai a diperleh dengan cara
$\begin{align*} U4 &= 17 \\ a+3b &= 17 \\ a+12 &= 17 \\ a &= 5 \\ \end{align*}$
maka nilai dari $U_25$ adalah
$\begin{align*} U_{25} &= a+24b \\ &= 5+24.4 \\ &= 5 + 96 \\ &= 101 \\ \end{align*}$
maka nilai dari $U_{25}=101$
--- Soal No 13 ---
penyelesaian dari sistem persamaan
$x+2y-3z=-4$
$2x-y+z=5$
$3x+2y+z=16$ adalah ... .
A. $(2,3,4)$
B. $(4,3,2)$
C. $(-2,3,4)$
D. $(-3,4,2)$
E. $(4,2,3)$
$x+2y-3z=-4$
$2x-y+z=5$
$3x+2y+z=16$ adalah ... .
A. $(2,3,4)$
B. $(4,3,2)$
C. $(-2,3,4)$
D. $(-3,4,2)$
E. $(4,2,3)$
Kunci : A. $(2,3,4)$
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan 2 di persamaan 1 maka diperoleh
$2x+4y-6z = -8 $
$\underline{2x-y+z = 5} _{-}$
$5y-7z=-13$.... $(4)$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan 3 di persamaan 1 maka diperoleh
$3x+6y-9z = -12 $
$\underline{3x+2y+z=16} _{-}$
$4y-10z=-28$ .... $(5)$
Ambil persamaan 4 dan 5, kemudian eliminasi nilai y dengan mengalikan silang koefisien y, sehingga diperoleh
$20y-28z = -52 $
$\underline{20y-50z=-140} _{-}$
$22z=88$
$z=4$
kemudian temukan nilai y dengan cara
$\begin{align*} 4y-10z &=-28 \\ 4y-10.4 &=-28 \\ 4y &=12 \\ y &= 3 \end{align*}$
kemudian temukan nilai x dengan cara
$\begin{align*} x+2y-3z &=-4 \\ x+2.3-3.4 &=-4 \\ x+6-12 &=-4 \\ x &= 2 \end{align*}$
Maka jawaban yang tepat adalah $A$
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan 2 di persamaan 1 maka diperoleh
$2x+4y-6z = -8 $
$\underline{2x-y+z = 5} _{-}$
$5y-7z=-13$.... $(4)$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan 3 di persamaan 1 maka diperoleh
$3x+6y-9z = -12 $
$\underline{3x+2y+z=16} _{-}$
$4y-10z=-28$ .... $(5)$
Ambil persamaan 4 dan 5, kemudian eliminasi nilai y dengan mengalikan silang koefisien y, sehingga diperoleh
$20y-28z = -52 $
$\underline{20y-50z=-140} _{-}$
$22z=88$
$z=4$
kemudian temukan nilai y dengan cara
$\begin{align*} 4y-10z &=-28 \\ 4y-10.4 &=-28 \\ 4y &=12 \\ y &= 3 \end{align*}$
kemudian temukan nilai x dengan cara
$\begin{align*} x+2y-3z &=-4 \\ x+2.3-3.4 &=-4 \\ x+6-12 &=-4 \\ x &= 2 \end{align*}$
Maka jawaban yang tepat adalah $A$
--- Soal No 14 ---
Diketahui sistem persamaan sebagai berikut
$-x+y-z=2$
$2x-2y-z=-1$
$3x+2y+z=6$ maka nilai dari $x+2y-2z$ adalah ... .
A. 5
B. -5
C. 4
D. -4
E. 3
$-x+y-z=2$
$2x-2y-z=-1$
$3x+2y+z=6$ maka nilai dari $x+2y-2z$ adalah ... .
A. 5
B. -5
C. 4
D. -4
E. 3
Kunci : A. 5
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan -2 di persamaan 1 maka diperoleh
$2x-2y+2z = -4 $
$\underline{2x-2y-z = -1} _{-}$
$3z=-3$
$z=-1$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan -3 di persamaan 1 maka diperoleh
$3x-3y+3z = -6 $
$\underline{3x+2y+z=6} _{-}$
$-5y+2z=-12$
$-5y+2(-1)=-12$
$-5y-2=-12$
$y=2$
Untuk menemukan nilai x ambil salah satu persamaan diawal diperoleh
$\begin{align*} -x+y-z &=2 \\ -x+2-(-1) &=2 \\ -x &=2 -3 \\ x &= 1 \end{align*}$
maka nilai dari $x+2y-2z=1+2.2-2(-1)=7$
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan -2 di persamaan 1 maka diperoleh
$2x-2y+2z = -4 $
$\underline{2x-2y-z = -1} _{-}$
$3z=-3$
$z=-1$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan -3 di persamaan 1 maka diperoleh
$3x-3y+3z = -6 $
$\underline{3x+2y+z=6} _{-}$
$-5y+2z=-12$
$-5y+2(-1)=-12$
$-5y-2=-12$
$y=2$
Untuk menemukan nilai x ambil salah satu persamaan diawal diperoleh
$\begin{align*} -x+y-z &=2 \\ -x+2-(-1) &=2 \\ -x &=2 -3 \\ x &= 1 \end{align*}$
maka nilai dari $x+2y-2z=1+2.2-2(-1)=7$
--- Soal No 15 ---
Pada suatu hari Adit, Bagas, dan Candra memanen mangga. Hasil kebun Candra lebih sedikit 15 kg dari hasil kebun Adit dan lebih banyak 15 kg dari hasil kebun Bagas. Jika jumlah hasil panen ketiga kebun tersebut 225 kg, maka hasil panen adit adalah ... .
A. 60
B. 90
C. 95
D. 97
E. 67
A. 60
B. 90
C. 95
D. 97
E. 67
Kunci : B. 90
Dari soal akan diperoleh sistem persamaan sebagai berikut, dengan memilsalkan adit adalah a, bagas adalah b dam candra adalah c
$\begin{align*} a-15 &= c \\ c-15 &=b \\ a+b+c &=225 \\ \end{align*}$
kemudian dengan metode substitusi akan diperoleh
$\begin{align*} a+b+c &=225 \\ a+(c-15)+(a-15) &=225 \\ a+((a-15)-15)+(a-15) &=225 \\ a+((a-30)+(a-15) &=225 \\ 3a-45 &=225 \\ 3a &=270 \\ a &= 90 \end{align*}$
maka jawaban yang tepat adalah $B$
Dari soal akan diperoleh sistem persamaan sebagai berikut, dengan memilsalkan adit adalah a, bagas adalah b dam candra adalah c
$\begin{align*} a-15 &= c \\ c-15 &=b \\ a+b+c &=225 \\ \end{align*}$
kemudian dengan metode substitusi akan diperoleh
$\begin{align*} a+b+c &=225 \\ a+(c-15)+(a-15) &=225 \\ a+((a-15)-15)+(a-15) &=225 \\ a+((a-30)+(a-15) &=225 \\ 3a-45 &=225 \\ 3a &=270 \\ a &= 90 \end{align*}$
maka jawaban yang tepat adalah $B$
--- Soal No 16 ---
Ayu, Bimo dan Candra berbelanja di sebuah toko secara bersamaan. ayu membeli 3 pensil, 4 buku tulis dan 1 penghapus. Bimo membeli 6 pensil, 2 buku tulis dan 1 penghapus. Candra membeli 2 pensil, 5 buku tulis dan 10 penghapus. dikasir Ayu membayar Rp. 83.000,00, Bimo membayar Rp. 86.000,00 dan Chandra membayar Rp. 158.000,00. berapa harga 1 penghapus ... .
A. Rp 9000
B. Rp 8000
C. Rp 7000
D. Rp 12000
E. Rp 6000
A. Rp 9000
B. Rp 8000
C. Rp 7000
D. Rp 12000
E. Rp 6000
Kunci : B. Rp 8000
degan memisalkan pensil adalah x, buku adalah y dan penghapus adalah z, maka akan diperoleh persamaan sebagai berikut $\begin{align*} 3x+4y+z &= 83.000 \\ 6x+2y+z &= 86.000 \\ 2x+5y+10z &=158.000 \\ \end{align*}$
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan 2 di persamaan 1 maka diperoleh
$6x+8y+2z = 166.000 $
$\underline{6x+2y+z = 86.000} _{-}$
$6y+z=80.000$ ..... $(4)$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan silang koefisiennya maka diperoleh
$6x+8y+2z = 166.000 $
$\underline{6x+15y+30z=474.000} _{-}$
$-7y-28z=-308.000$ ..... $(5)$
ambil persamaan 3 dan 4 dengan mengalikan silang koefisien y diperoleh
$42y+7z = 560.000 $
$\underline{-42y-168z=-1.848.000} _{+}$
$-161z=-1.288.000$
$z=8.000$
maka harga sebuah penghapus adalah $8.000$
degan memisalkan pensil adalah x, buku adalah y dan penghapus adalah z, maka akan diperoleh persamaan sebagai berikut $\begin{align*} 3x+4y+z &= 83.000 \\ 6x+2y+z &= 86.000 \\ 2x+5y+10z &=158.000 \\ \end{align*}$
Ambil persamaan 1 dan 2, kemudian samakan koefisien $x$ dengan mengalikan 2 di persamaan 1 maka diperoleh
$6x+8y+2z = 166.000 $
$\underline{6x+2y+z = 86.000} _{-}$
$6y+z=80.000$ ..... $(4)$
Ambil persamaan 1 dan 3, kemudian samakan koefisien $x$ dengan mengalikan silang koefisiennya maka diperoleh
$6x+8y+2z = 166.000 $
$\underline{6x+15y+30z=474.000} _{-}$
$-7y-28z=-308.000$ ..... $(5)$
ambil persamaan 3 dan 4 dengan mengalikan silang koefisien y diperoleh
$42y+7z = 560.000 $
$\underline{-42y-168z=-1.848.000} _{+}$
$-161z=-1.288.000$
$z=8.000$
maka harga sebuah penghapus adalah $8.000$
--- Soal No 17 ---
Perhatikan gambar di bawah
Gambar diatas adalah gambar dari pertaksamaan berikut
$5x+y > 10$
$x+2y < 8$
$y >2$
$x > 0$
daerah penyelesaianya ditunjukan oleh nomor ...
A. I
B. II
C. III
D. IV
E. V
$5x+y > 10$
$x+2y < 8$
$y >2$
$x > 0$
daerah penyelesaianya ditunjukan oleh nomor ...
A. I
B. II
C. III
D. IV
E. V
Kunci : C. III
Dalam mengarsir daerah penyelesaian hanya perlu melihat tandanya, jika lebih besar maka arsisr ke kanan atau atas, dan lebih kecil ke kiri atau ke bawah. Namun agar lebih mudah dalam menggambar dalam hal ini akan di arsir kebalikannya atau daerah yang salah, sehingga daerah yang bersih adalah penyelesaianya. maka gambarnya adalah sebagai berikut.
maka jawaban yang paling tepat adalah III
Dalam mengarsir daerah penyelesaian hanya perlu melihat tandanya, jika lebih besar maka arsisr ke kanan atau atas, dan lebih kecil ke kiri atau ke bawah. Namun agar lebih mudah dalam menggambar dalam hal ini akan di arsir kebalikannya atau daerah yang salah, sehingga daerah yang bersih adalah penyelesaianya. maka gambarnya adalah sebagai berikut.
maka jawaban yang paling tepat adalah III
--- Soal No 18 ---
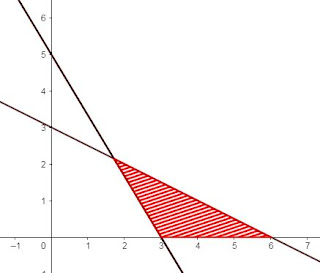
Perhatikan gambar berikut
pertaksamaan yang sesuai dengan gambar diatas adalah ... .
A. $4x+5y \geq 20$
B. $x+y \geq 5$
C. $4x+5y \leq 20$
D. $5x+4y \geq 20$
E. $5x+4y \leq 20$
pertaksamaan yang sesuai dengan gambar diatas adalah ... .
A. $4x+5y \geq 20$
B. $x+y \geq 5$
C. $4x+5y \leq 20$
D. $5x+4y \geq 20$
E. $5x+4y \leq 20$
Kunci : D. $5x+4y \geq 20$
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
dari kedua sifat tersebut diperoleh pertaksamaan $5x+4y \geq 20$
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
dari kedua sifat tersebut diperoleh pertaksamaan $5x+4y \geq 20$
--- Soal No 19 ---
Sistem pertaksamaan yang sesuai dengan daerah penyelesaian diatas adalah ... .
A. $x+2y \leq 6; 5x+3y \leq 15 ; x \geq 0 ; y \geq 0$
B. $x+2y \leq 6; 3x+5y \leq 15 ; x \geq 0 ; y \geq 0$
C. $x+2y \geq 6; 5x+3y \leq 15 ; x \geq 0 ; y \geq 0$
D. $x+2y \geq 6; 3x+5y \leq 15 ; x \geq 0 ; y \geq 0$
E. $x+2y \leq 6; 5x+3y \geq 15 ; x \geq 0 ; y \geq 0$
A. $x+2y \leq 6; 5x+3y \leq 15 ; x \geq 0 ; y \geq 0$
B. $x+2y \leq 6; 3x+5y \leq 15 ; x \geq 0 ; y \geq 0$
C. $x+2y \geq 6; 5x+3y \leq 15 ; x \geq 0 ; y \geq 0$
D. $x+2y \geq 6; 3x+5y \leq 15 ; x \geq 0 ; y \geq 0$
E. $x+2y \leq 6; 5x+3y \geq 15 ; x \geq 0 ; y \geq 0$
Kunci : E. $x+2y \leq 6; 5x+3y \geq 15 ; x \geq 0 ; y \geq 0$
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. Kemudian lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
dari dua point diatas maka dapat dibentuk pertaksamaan sebagai berikut.
$x+2y \leq 6$
$3x + 5y \geq 15 $
$y \geq 0$
$x \geq 0$
maka jawaban yang tepat adalah E
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. Kemudian lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
dari dua point diatas maka dapat dibentuk pertaksamaan sebagai berikut.
$x+2y \leq 6$
$3x + 5y \geq 15 $
$y \geq 0$
$x \geq 0$
maka jawaban yang tepat adalah E
--- Soal No 20 ---
Perhatikan gambar berikut
gambar di atas adalah gambar dari pertaksaman berikut
$3x+2y \leq 36$
$x+2y \geq 20$
$x \geq 0$
$y \geq 0$
maka penyelesaianya ditunjukan oleh nomor berapa ...
A. I
B. II
C. III
D. IV
E. V
gambar di atas adalah gambar dari pertaksaman berikut
$3x+2y \leq 36$
$x+2y \geq 20$
$x \geq 0$
$y \geq 0$
maka penyelesaianya ditunjukan oleh nomor berapa ...
A. I
B. II
C. III
D. IV
E. V
Kunci :
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. Kemudian lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
maka dengan kedua langkah diatas menentukan daerah arsiran bisa dilihat dari tanda pertaksamaannya. ingat dalam hal ini akan di arsisr daerah yang salah maka untuk kurva
$3x+2y \leq 36$ arsir ke kanan
$x+2y \geq 20$ arsisr ke bawah
$x \geq 0$ arisir ke kiri
$y \geq 0$ arsir ke bawah
maka Daerah Penyelesaian yang tepat adalah daerah nomor II
1. Untuk menyelesaiakn soal ini hanya perlu melihat titik potong dengan sumbu-sumbunya. Misal jika tipot garis di titik $(a,0)$ dan $(0,b)$ maka persamaan garisnya adalah $bx+ay=a.b$.
2. Kemudian lihat arsiran, jika ke kanan maka tanda lebih dari dan ke kiri kurang dari. dilihat dari garis ke daerah arsiran
maka dengan kedua langkah diatas menentukan daerah arsiran bisa dilihat dari tanda pertaksamaannya. ingat dalam hal ini akan di arsisr daerah yang salah maka untuk kurva
$3x+2y \leq 36$ arsir ke kanan
$x+2y \geq 20$ arsisr ke bawah
$x \geq 0$ arisir ke kiri
$y \geq 0$ arsir ke bawah
maka Daerah Penyelesaian yang tepat adalah daerah nomor II
--- Soal No 21 ---
Bila $x_1$ dan $x_2$ adalah akar-akar persamaan kuadrat $x^2-6x-5=0$ maka nilai dari $x_1^2+x_2^2$ adalah ... .
A. 26
B. 31
C. 37
D. 41
E. 46
A. 26
B. 31
C. 37
D. 41
E. 46
Kunci : E. 46
Sesuai teorema vieta diperoleh
$x_1+x_2=\frac{-b}{a}=6$
$x_1.x_2=\frac{c}{a}=-5$
sehingga untuk menjawan spal kita akan mulai dari mengkuadratkan jumlah akar-akarnya yaitu.
$\begin{align*} x_1+x_2 &=6 \\ (x_1+x_2)^2 &=6^2 \\ x_1^2+2.x_1.x_2+x_2^2 &= 36 \\ x_1^2+2.(-5)+x_2^2 &= 36 \\ x_1^2-10+x_2^2 &= 36 \\ x_1^2+x_2^2 &= 46 \end{align*}$
maka jawaban yang paling tepat adalah 46
Sesuai teorema vieta diperoleh
$x_1+x_2=\frac{-b}{a}=6$
$x_1.x_2=\frac{c}{a}=-5$
sehingga untuk menjawan spal kita akan mulai dari mengkuadratkan jumlah akar-akarnya yaitu.
$\begin{align*} x_1+x_2 &=6 \\ (x_1+x_2)^2 &=6^2 \\ x_1^2+2.x_1.x_2+x_2^2 &= 36 \\ x_1^2+2.(-5)+x_2^2 &= 36 \\ x_1^2-10+x_2^2 &= 36 \\ x_1^2+x_2^2 &= 46 \end{align*}$
maka jawaban yang paling tepat adalah 46
--- Soal No 22 ---
Jika 2 dan 3 adalah akar persamaan kuadrat, maka persamaan kuadrat yang dimaksud adalah ... .
A. $x^2+x+5=0$
B. $x^2+6x+5=0$
C. $x^2+5x-6=0$
D. $x^2-5x+6=0$
E. $x^2-x+5=0$
A. $x^2+x+5=0$
B. $x^2+6x+5=0$
C. $x^2+5x-6=0$
D. $x^2-5x+6=0$
E. $x^2-x+5=0$
Kunci : D. $x^2-5x+6=0$
karena akar-akar persamaa kudarat telah ada, maka persamaan kuadratnya dapat dicari dengan cara
$\begin{align*} (x-3)(x-2) &=0 \\ x^2-3x-2x+6 &=0 \\ x^2-5x+6 =0 \end{align*}$
jawaban yang paling tepat adalah D. $x^2-5x+6=0$
karena akar-akar persamaa kudarat telah ada, maka persamaan kuadratnya dapat dicari dengan cara
$\begin{align*} (x-3)(x-2) &=0 \\ x^2-3x-2x+6 &=0 \\ x^2-5x+6 =0 \end{align*}$
jawaban yang paling tepat adalah D. $x^2-5x+6=0$
--- Soal No 23 ---
Grafik fungsi $y=x^2-4x+a$ tidak akan memotong sumbu x di dua titik jika ... .
A. $a < 0$
B. $a < 4$
C. $ a \leq 4$
D. $a > 0$
E. $a \geq 4$
A. $a < 0$
B. $a < 4$
C. $ a \leq 4$
D. $a > 0$
E. $a \geq 4$
Kunci : E. $a \geq 4$
Grafik fungsi kuadrat tidak akan memotong sumbu x di dua titik jika diskriminan lebih dari atau sama dengan nol, maka
$\begin{align*} D &\leq 0 \\ b^2-4ac &\leq 0 \\ (-4)^2-4.1.a &\leq 0 \\ 16-4a &\leq 0 \\ 4a &\geq 16 \\ a &\geq 4 \end{align*}$
maka jawaban yang tepat adalah E
Grafik fungsi kuadrat tidak akan memotong sumbu x di dua titik jika diskriminan lebih dari atau sama dengan nol, maka
$\begin{align*} D &\leq 0 \\ b^2-4ac &\leq 0 \\ (-4)^2-4.1.a &\leq 0 \\ 16-4a &\leq 0 \\ 4a &\geq 16 \\ a &\geq 4 \end{align*}$
maka jawaban yang tepat adalah E
--- Soal No 24 ---
Titik puncak dari parabola $y=2x^2-12x+14$ adalah ... .
A. $(3,4)$
B. $(3,-4)$
C. $(6,4)$
D. $(6,-4)$
E. $(3,6)$
A. $(3,4)$
B. $(3,-4)$
C. $(6,4)$
D. $(6,-4)$
E. $(3,6)$
Kunci : B. $(3,-4)$
titik puncak dari parabola diperoleh dengan cara $\left ( -\frac{b}{2a},\frac{D}{-4a} \right )$ maka
$\left ( -\frac{b}{2a},\frac{D}{-4a} \right ) $
$\left ( -\frac{-12}{2.2},\frac{(-12)^2-4.2.14}{-4.2} \right )$
$\left ( 3,\frac{32}{-8} \right )$
$\left ( 3,-4 \right )$
jawban yang tepat adalah B
titik puncak dari parabola diperoleh dengan cara $\left ( -\frac{b}{2a},\frac{D}{-4a} \right )$ maka
$\left ( -\frac{b}{2a},\frac{D}{-4a} \right ) $
$\left ( -\frac{-12}{2.2},\frac{(-12)^2-4.2.14}{-4.2} \right )$
$\left ( 3,\frac{32}{-8} \right )$
$\left ( 3,-4 \right )$
jawban yang tepat adalah B
--- Soal No 25 ---
Jika parabola $y=x^2-px+7$ puncaknya memiliki absis 4, maka ordinatnya adalah... .
A. -9
B. -8
C. 0
D. 8
E. 9
A. -9
B. -8
C. 0
D. 8
E. 9
Kunci : A. -9
Temukan nilai p dengan rumus sumbu simetri persamaan kuadrat yaitu.
$\begin{align*} \frac{-b}{2a} &= 4 \\ \frac{-(-p)}{2.1} &= 4 \\ p &= 8 \end{align*}$
kemudian nilai ordinatnya hanya perlu mengganti x atau absisnya dengan 4, sehingga diperoleh nilai ordinatnya adalah
$\begin{align*} y &= x^2-px+7 \\ &= x^2-8x+7 \\ &= (4)^2-8.4+7 \\ &= -9 \end{align*}$
jadi jawban yang tepat adalah A
Temukan nilai p dengan rumus sumbu simetri persamaan kuadrat yaitu.
$\begin{align*} \frac{-b}{2a} &= 4 \\ \frac{-(-p)}{2.1} &= 4 \\ p &= 8 \end{align*}$
kemudian nilai ordinatnya hanya perlu mengganti x atau absisnya dengan 4, sehingga diperoleh nilai ordinatnya adalah
$\begin{align*} y &= x^2-px+7 \\ &= x^2-8x+7 \\ &= (4)^2-8.4+7 \\ &= -9 \end{align*}$
jadi jawban yang tepat adalah A










Tidak ada komentar:
Posting Komentar