 |
Berikut disajikan soal Olimpiade Matematika SMP yang dikumpulkan dari berbagai sumber, baik dari buku, internet, menanyakan ke peserta lomba atau dari sumber lainnya. Dalam penyajiannya juga disertakan petunjuk cara pengerjaan, kunci dan video pembahasan di setiap soalnya, Hal ini dimaksudkan agar siswa bisa mengerjakan soal sesuai dengan kebutuhannya serta Semoga postingan ini dapat membatu siswa menuju medali olimpiade yang sudah didambakan. |
--- Soal No 1 ---
Urutkan bilangan - bilangan $2^{5555}, 5^{2222}$ dan $3^{3333}$ dari yang terkecil sampai yang terbesar ... .
A. $2^{5555}, 5^{2222}, 3^{3333}$
B. $5^{2222}, 3^{3333}, 2^{5555}$
C. $3^{3333}, 2^{5555}, 5^{2222}$
D. $5^{2222}, 2^{5555}, 3^{3333}$
E. $3^{3333}, 5^{2222}, 2^{5555}$
A. $2^{5555}, 5^{2222}, 3^{3333}$
B. $5^{2222}, 3^{3333}, 2^{5555}$
C. $3^{3333}, 2^{5555}, 5^{2222}$
D. $5^{2222}, 2^{5555}, 3^{3333}$
E. $3^{3333}, 5^{2222}, 2^{5555}$
Kunci : B. $5^{2222}, 3^{3333}, 2^{5555}$
Petunjuk !
Buatlah pangkat pada setiap bilangan tersebut sama, sehingga jika pangkat sudah sama maka hanya perlu diurutkan bilangan yang dipangkatkan saja.
Petunjuk !
Buatlah pangkat pada setiap bilangan tersebut sama, sehingga jika pangkat sudah sama maka hanya perlu diurutkan bilangan yang dipangkatkan saja.
--- Soal No 2 ---
Misalkan a,b dan c adalh bilangan bulat, maka pernyataan berikut yang bernilai salah adalah ... .
A. Jika a membagi b dan b membagi c, maka a membagi c
B. Jika a membagi b dan c, maka a membagi b + c
C. Jika a membagi b dan c, maka a membagi bc
D. Jika a membagi c dan b, maka ab membagi c
E. jika a membagi b, maka a membagi bc
A. Jika a membagi b dan b membagi c, maka a membagi c
B. Jika a membagi b dan c, maka a membagi b + c
C. Jika a membagi b dan c, maka a membagi bc
D. Jika a membagi c dan b, maka ab membagi c
E. jika a membagi b, maka a membagi bc
Kunci : D. Jika a membagi c dan b, maka ab membagi c
Petunjuk !
1. jawaban no a salah karena a haruslah membagi c
2. jawaban no b salah karena a haruslah membagi b + c
3. jawaban no c salah karena a haruslah membagi bc
4. benar
5. jawaban no e salah karena a haruslah membagi bc
Petunjuk !
1. jawaban no a salah karena a haruslah membagi c
2. jawaban no b salah karena a haruslah membagi b + c
3. jawaban no c salah karena a haruslah membagi bc
4. benar
5. jawaban no e salah karena a haruslah membagi bc
--- Soal No 3 ---
A. $360$
B. $540$
C. $720$
D. $900$
E. $1.260$
Kunci : E. $1.260$
Petunjuk !
Bagilah bangun menjadi beberapa segitiga, dan ingat bahwa jumlah sudut pada sebuah segitiga sama dengan 180 derajat. maka dengan konsep tersebut soal ini bisa dijawab.
Petunjuk !
Bagilah bangun menjadi beberapa segitiga, dan ingat bahwa jumlah sudut pada sebuah segitiga sama dengan 180 derajat. maka dengan konsep tersebut soal ini bisa dijawab.
--- Soal No 4 ---
Jika f adalah suatu fungsi dari himpunan bilangan asli ke bilangan asli yang memenuhi $f(x)+f(x+1)=2x^2$ dan $f(31)=99$, maka tentukan nilai dari $f(99)$... .
A. $8.673$
B. $8.772$
C. $8.871$
D. $9.505$
E. $6.240$
A. $8.673$
B. $8.772$
C. $8.871$
D. $9.505$
E. $6.240$
Kunci : C. $8.871$
Petunjuk !
1. jika dicari secara sekalian dengan mengambil nilai $x=99$ atau $x=98$ maka kita memerlukan nilai suatu fungsi yang belum diketahui, oleh sebab itu sal ini bisa disiasati dengan menggunakan informasi yang ada disoal yaitu $f(31)=99$
2. ambil nilai x ganjik dari 31 hingga 99, kemudan jumlahkan fungsi, maka akan diperoleh suatu persamaan tertentu
3. ambil nilai x genap dari 32 hingga 98, kemudan jumlahkan fungsi, maka akan diperoleh suatu persamaan tertentu
4. kurangi persamaan pada point 3 dengan persamaan pada point kemudian yang mengakibatkan hanya menyisahkan bentuk $f(99)+f(31)=$ suatu deret tertentu
5. selesaikan persamaan dengan memanfaatkan rumus barisan dan deret.
Petunjuk !
1. jika dicari secara sekalian dengan mengambil nilai $x=99$ atau $x=98$ maka kita memerlukan nilai suatu fungsi yang belum diketahui, oleh sebab itu sal ini bisa disiasati dengan menggunakan informasi yang ada disoal yaitu $f(31)=99$
2. ambil nilai x ganjik dari 31 hingga 99, kemudan jumlahkan fungsi, maka akan diperoleh suatu persamaan tertentu
3. ambil nilai x genap dari 32 hingga 98, kemudan jumlahkan fungsi, maka akan diperoleh suatu persamaan tertentu
4. kurangi persamaan pada point 3 dengan persamaan pada point kemudian yang mengakibatkan hanya menyisahkan bentuk $f(99)+f(31)=$ suatu deret tertentu
5. selesaikan persamaan dengan memanfaatkan rumus barisan dan deret.
--- Soal No 5 ---
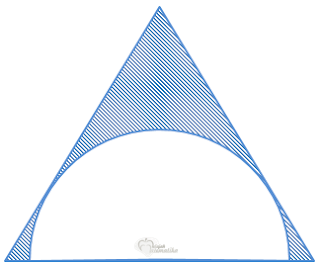
Diketahui sustu segitiga sama sisi dan setengah lingkaran seperti pada gambar di bawah ini.
Jika panjang sisi segitiga tersebut adalah 14cm, maka luas daerah di dalam segitiga dan luar setenagh lingkaran adalah ... $Cm^2$ ... .
Jika panjang sisi segitiga tersebut adalah 14cm, maka luas daerah di dalam segitiga dan luar setenagh lingkaran adalah ... $Cm^2$ ... .
A. $49\sqrt{3}-14 \pi$
B. $49\sqrt{3}-12 \pi$
C. $49\sqrt{3}-18 \frac{3}{8} \pi$
D. $98\sqrt{3}-27 \pi$
E. $98\sqrt{3}-12 \pi$
B. $49\sqrt{3}-12 \pi$
C. $49\sqrt{3}-18 \frac{3}{8} \pi$
D. $98\sqrt{3}-27 \pi$
E. $98\sqrt{3}-12 \pi$
Kunci : C. $49\sqrt{3}-18 \frac{3}{8} \pi$
Petunjuk !
1. soal ini dapat diselesaikan dengan konsep kesamaan pytagoras atau bisa juga dengan konsep kesebangunan, pada petunjuk kali ini akan diselesaikan dengan konsep kesebangunan. misalkan nama segitiganya ABC dengan puncak di A, kemudian titik D adalah garis yang di tarik dari Cke pusat lingkaran dan E adalah titik singgung sisi lingkaran dengan sisi AB.
2. cari terlebih dahulu panjang AD dengan konsep pytagoras.
3. kemudian perhatikan segitiga ABD dan BDE kedua segitiga sebangun, maka terapkan kosep kesebangunan maka nilai r akan ditemukan.
4. jika r ada maka soal bisa diselesaikan
Petunjuk !
1. soal ini dapat diselesaikan dengan konsep kesamaan pytagoras atau bisa juga dengan konsep kesebangunan, pada petunjuk kali ini akan diselesaikan dengan konsep kesebangunan. misalkan nama segitiganya ABC dengan puncak di A, kemudian titik D adalah garis yang di tarik dari Cke pusat lingkaran dan E adalah titik singgung sisi lingkaran dengan sisi AB.
2. cari terlebih dahulu panjang AD dengan konsep pytagoras.
3. kemudian perhatikan segitiga ABD dan BDE kedua segitiga sebangun, maka terapkan kosep kesebangunan maka nilai r akan ditemukan.
4. jika r ada maka soal bisa diselesaikan
--- Soal No 6 ---
Pada Sebuah lapangan berbentuk persegi dengan titik Sudutnya di ABCD, kemudian seekor sapi diikat di pinggir lapangan dan misaklan di titik E yang berada di sisi AD sehingga panjang AE = 2 m. Apabila panjang sisi lapangan adalah 7 m dan panjang tali pengingat sapinya adalah 4 m, maka berapakah luas rumput yang bisa dimakan oleh sapi... .
A. $2\sqrt{3}+\frac{16 \pi}{3}$
B. $2\sqrt{3}+4 \pi$
C. $2\sqrt{2}+\frac{16 \pi}{3}$
D. $4 + 4 \pi$
E. $8 + 8 \pi$
A. $2\sqrt{3}+\frac{16 \pi}{3}$
B. $2\sqrt{3}+4 \pi$
C. $2\sqrt{2}+\frac{16 \pi}{3}$
D. $4 + 4 \pi$
E. $8 + 8 \pi$
Kunci : A. $2\sqrt{3}+\frac{16 \pi}{3}$
Petunjuk !
1. Ilusrasikan soal pada gambar !
2. buatlah setengah lingkaran yang berpusat di E sehingga memotong sisi persegi AB di titik E. dan lihatlah segitiga AEF, jika dicari perbandingan nilai cosinus dari sudut AEF, maka diperoleh besar sudutnya adalah 60 derajat, akibatnya besar sudut DEF adalah 120 derajat
3. maka luas daerah yang bisa dimakan oleh sapi adalah luas segitiga AEF + luas juring DEF.
Petunjuk !
1. Ilusrasikan soal pada gambar !
2. buatlah setengah lingkaran yang berpusat di E sehingga memotong sisi persegi AB di titik E. dan lihatlah segitiga AEF, jika dicari perbandingan nilai cosinus dari sudut AEF, maka diperoleh besar sudutnya adalah 60 derajat, akibatnya besar sudut DEF adalah 120 derajat
3. maka luas daerah yang bisa dimakan oleh sapi adalah luas segitiga AEF + luas juring DEF.
--- Soal No 7 ---
A. $4$
B. $16$
C. $22$
D. $60$
E. $80$
Kunci : D. $60$
Petunjuk !
1. Gunakanlah bobot grap dalam menyelesaikan soal ini. dimana bobot graph adalah besar bobot sisi yang di lalui oleh suatu jalur dari A ke B. Misal ambil conoth 1 persegi paling pokok kanan di soal, kita misalkan PQRS adalah nama persegi. dengan PR dan QS adalah diagonal
2. Bobot grap/ banyak jalur dari P ke Q hanya ada 1 kita isi angka 1 di titik Q, begitupula dari P ke S.
3. kemudian bobot dari P ke R ada dua jalur yaitu melalui Q atau S maka isi tanda 2 di titik R
4. ulangi langkah itu hingga sampai titik Q.
Petunjuk !
1. Gunakanlah bobot grap dalam menyelesaikan soal ini. dimana bobot graph adalah besar bobot sisi yang di lalui oleh suatu jalur dari A ke B. Misal ambil conoth 1 persegi paling pokok kanan di soal, kita misalkan PQRS adalah nama persegi. dengan PR dan QS adalah diagonal
2. Bobot grap/ banyak jalur dari P ke Q hanya ada 1 kita isi angka 1 di titik Q, begitupula dari P ke S.
3. kemudian bobot dari P ke R ada dua jalur yaitu melalui Q atau S maka isi tanda 2 di titik R
4. ulangi langkah itu hingga sampai titik Q.
--- Soal No 8 ---
Desi merayakan hari ulang tahun pada 27 desember 2006. Jika pada hari tersebut usia deni sama dengan julah digit dari angka tahun kelahiranya, maka desi lahir pada tahun ... .
A. $1994$
B. $1989$
C. $1979$
D. $1992$
E. $1984$
A. $1994$
B. $1989$
C. $1979$
D. $1992$
E. $1984$
Kunci : E. $1984$
Petunjuk !
1. misalkan desi lahir tahun 19ab dengan a dan b adalah bilangan cacah 1 digit, maka 19ab = 1900 + 10.a +b
2. karena umur dan jumlah tahun lahir sama maka jumlah digit tahun lahir = umur = tahun 2006 - tahun lahir
3. dari point 2 akan diperoleh suatu persamaan dalam bentuk ab, uji nilai a dan b dan temukan nilai yang cocok.
Petunjuk !
1. misalkan desi lahir tahun 19ab dengan a dan b adalah bilangan cacah 1 digit, maka 19ab = 1900 + 10.a +b
2. karena umur dan jumlah tahun lahir sama maka jumlah digit tahun lahir = umur = tahun 2006 - tahun lahir
3. dari point 2 akan diperoleh suatu persamaan dalam bentuk ab, uji nilai a dan b dan temukan nilai yang cocok.
--- Soal No 9 ---
Suatu barisan hanya terdiri dari angka 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, ..., maka suku ke100 bilangan tersebut adalah ... .
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Kunci : D. $4$
Petunjuk !
1. perhatikan banyaknya angka 1,2,3,4,5 bertambah secara konsisten, 1 ada 1, 2 ada 2, 3 ada 3, 4 ada 4, 5 ada 5 kemudian kembali lagi 1 ada 6 dan seterusnya, maka anggaplah jumlah nya mengikuti barisan 1, 2, 3, 4, 5, 6, ... maka cari cari dimana jumlah nya sama dengan 100.
2. untuk mencari jumlahnya secara cepat bisa terapkan rumus jumlah deret bilaangan itu adalag $\frac{n(n+1)}{2}$
Petunjuk !
1. perhatikan banyaknya angka 1,2,3,4,5 bertambah secara konsisten, 1 ada 1, 2 ada 2, 3 ada 3, 4 ada 4, 5 ada 5 kemudian kembali lagi 1 ada 6 dan seterusnya, maka anggaplah jumlah nya mengikuti barisan 1, 2, 3, 4, 5, 6, ... maka cari cari dimana jumlah nya sama dengan 100.
2. untuk mencari jumlahnya secara cepat bisa terapkan rumus jumlah deret bilaangan itu adalag $\frac{n(n+1)}{2}$
--- Soal No 10 ---
konstanta dari $\left ( 3x^{3}-\frac{2}{x} \right )^{8}$ adalah ... .
A. $14.328$
B. $15.552$
C. $16.112$
D. $16.128$
E. $17.128$
A. $14.328$
B. $15.552$
C. $16.112$
D. $16.128$
E. $17.128$
Kunci : D. $16.128$
Petunjuk !
1. ingatlah bentuk theorema binomial yaitu $\left ( a+b \right )^{n}=\sum_{k=0}^{n}\binom{n}{k}.a^{n-k}.b^{k}$
2. jika bentuk binomial dan bentuk di soal disamanak maka diperoleh $a=3x^{3}$ dan $b=\frac{2}{x}$ dan jika di substitusi ke bentuk pada point 1 maka kita perlu menemukan nilai k yang memenuhi agar nilai variabel x hilang.
3. ada banyak cara menemukan nilai k, salah satunya membuat pangkatnya =0. Selain itu kita bisa memperkirakan nilainya agar hanya meninggalkan konstanta.
Petunjuk !
1. ingatlah bentuk theorema binomial yaitu $\left ( a+b \right )^{n}=\sum_{k=0}^{n}\binom{n}{k}.a^{n-k}.b^{k}$
2. jika bentuk binomial dan bentuk di soal disamanak maka diperoleh $a=3x^{3}$ dan $b=\frac{2}{x}$ dan jika di substitusi ke bentuk pada point 1 maka kita perlu menemukan nilai k yang memenuhi agar nilai variabel x hilang.
3. ada banyak cara menemukan nilai k, salah satunya membuat pangkatnya =0. Selain itu kita bisa memperkirakan nilainya agar hanya meninggalkan konstanta.
--- Soal No 11 ---
Banyaknya bilangan asli yang kurang dari 10.000 dengan jumlah digit pertama dan digit terakhirnya sama dengan 11 adalah ... .
A. $999$
B. $888$
C. $800$
D. $444$
E. $400$
A. $999$
B. $888$
C. $800$
D. $444$
E. $400$
Kunci : B. $888$
Petunjuk !
1. bilangan yang kurang dari 10.000 terdiri dari bilagan ribuan, ratusan dan puluhan. Temukan terlebih dahulu pasangan bilangan yang membuat digit pertama dan terakhirnya berjumlah 11
2. gunakan kaidah cacah unutk menemukan banyak bilangan masing-masing untuk bilangan ribuan, ratusan dan puluhan.
3. jumlahkan semua kemungkinanya.
Petunjuk !
1. bilangan yang kurang dari 10.000 terdiri dari bilagan ribuan, ratusan dan puluhan. Temukan terlebih dahulu pasangan bilangan yang membuat digit pertama dan terakhirnya berjumlah 11
2. gunakan kaidah cacah unutk menemukan banyak bilangan masing-masing untuk bilangan ribuan, ratusan dan puluhan.
3. jumlahkan semua kemungkinanya.
--- Soal No 12---
A. $12$
B. $18$
C. $20$
D. $22$
E. $24$
Kunci : E. $24$
Petunjuk !
1. Perhatikan segitiga TUR dan TPS adalah dua buah segitiga sebangun, maka melali konsep kesebangunan diperoleh perbandingan RU : PS dan mengakibatkan RU = UQ
2. Perhatikan pula segitiga VQU dan segitiga VPS adalah dua buah segitiga yang sebangun, maka dengan informasi ini diperoleh perbandingan yang memuat panjang UV, temukan nilai UV
Petunjuk !
1. Perhatikan segitiga TUR dan TPS adalah dua buah segitiga sebangun, maka melali konsep kesebangunan diperoleh perbandingan RU : PS dan mengakibatkan RU = UQ
2. Perhatikan pula segitiga VQU dan segitiga VPS adalah dua buah segitiga yang sebangun, maka dengan informasi ini diperoleh perbandingan yang memuat panjang UV, temukan nilai UV
--- Soal No 13 ---
JIka bilangan 123.456.789 dikalikan dengan bilangan 999.999.999 maka banyak angka 9 dari hasil perkalian tersebut adalah ... .
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
Kunci : A. $0$
Petunjuk !
misalkan bilangan 999.999.999 = 100.000.000 -1, kemudian kalikan dan temukan hasil yang diinginkan oleh soalnya.
Petunjuk !
misalkan bilangan 999.999.999 = 100.000.000 -1, kemudian kalikan dan temukan hasil yang diinginkan oleh soalnya.
--- Soal No 14 ---
A. $75$
B. $55$
C. $45$
D. $43$
E. $57$
Kunci : E. $57$
Petunjuk !
Temukan faktor dari 360, kemudian susun angka dalam kotak agar setiap 5 kotak berurutan memiliki hasil kali 360.
Petunjuk !
Temukan faktor dari 360, kemudian susun angka dalam kotak agar setiap 5 kotak berurutan memiliki hasil kali 360.
--- Soal No 15 ---
di laboratorium terdapat 6 batang kayu sejenis yang panjangnya berturut-turut adalah 2dm, 4dm, 4dm, 10dm, 22dm dan 37dm. Jika keenam batang kayu tesebut harus digunakan unutk membuat trapesium sama kaki, maka banyak trapesium sama kaki yang dapat dibuat tanpa memotong kayu adalah ... .
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Kunci : C. $3$
Petunjuk !
Temukan kemungkinan yang terjadi dengan catatatan bahwa kayu yang ada tidak boleh dipotong, namun boleh disambung tanpa ada batas sambungan, asalkan bentuknya trapesium
Petunjuk !
Temukan kemungkinan yang terjadi dengan catatatan bahwa kayu yang ada tidak boleh dipotong, namun boleh disambung tanpa ada batas sambungan, asalkan bentuknya trapesium
--- Soal No 16 ---
A. $112$
B. $145$
C. $155$
D. $154$
E. $120$
Kunci : B. $145$
Petunjuk !
1. Jika dicari, maka cacahlah atau temukan semua ukuran persegi yang dimaksud dari ukuran 1x1 hingga 9x9 yang erada di dalam persegi sesuai syarat pada soal. maka banyak persegi akan membentuk pola tertentu.
2. jika sudah ditemukan polanya, cobalah analisis dan terapkan rumus deret aritamatika atau geometri.
Petunjuk !
1. Jika dicari, maka cacahlah atau temukan semua ukuran persegi yang dimaksud dari ukuran 1x1 hingga 9x9 yang erada di dalam persegi sesuai syarat pada soal. maka banyak persegi akan membentuk pola tertentu.
2. jika sudah ditemukan polanya, cobalah analisis dan terapkan rumus deret aritamatika atau geometri.
Tidak ada komentar:
Posting Komentar