| Berikut disajikan soal Olimpiade Matematika SMP yang dikumpulkan dari berbagai sumber, baik dari buku, internet, menanyakan ke peserta lomba atau dari sumber lainnya. Dalam penyajiannya juga disertakan petunjuk cara pengerjaan, kunci dan video pembahasan di setiap soalnya, Hal ini dimaksudkan agar siswa bisa mengerjakan soal sesuai dengan kebutuhannya serta Semoga postingan ini dapat membatu siswa menuju medali olimpiade yang sudah didambakan. |
--- Soal No 1 ---
Sekumpulan data terdiri dari 5 bilangan asli yang memiliki rata-rata 8 dan rentang $($ selisih data terbesar dan data terkecilnya$)$ adalah 12. Bilangan asli terkecil yang tidak mungkin menjadi anggota dari kumpulan tersebut adalah... .
A. $1$
B. $20$
C. $18$
D. $6$
E. $15$
A. $1$
B. $20$
C. $18$
D. $6$
E. $15$
Kunci : C. $18$
Petunjuk !
1. Ingatlah bahwa agar terbentuk data dengan rata-rata terkecil maka nilai terbesar hanya ada satu dan sisanya bilangan yang paling kecil. misalkan bilangan yang paling kecil itu adalah variabel tertentu.
2. pada point 1 nilai terbesarnya sendiri yang paling besar karena ada syarat bahawa rentangannya atau selisih nilai terkecil dan terbesarnya
3. gunakan kedua cara diatas, maka nilainya bisa ditentukan.
Petunjuk !
1. Ingatlah bahwa agar terbentuk data dengan rata-rata terkecil maka nilai terbesar hanya ada satu dan sisanya bilangan yang paling kecil. misalkan bilangan yang paling kecil itu adalah variabel tertentu.
2. pada point 1 nilai terbesarnya sendiri yang paling besar karena ada syarat bahawa rentangannya atau selisih nilai terkecil dan terbesarnya
3. gunakan kedua cara diatas, maka nilainya bisa ditentukan.
--- Soal No 2 ---
Sepuluh pasang suami istri mengikuti suatu pesta, kemudian mereka saling berjabat tangan satu sama lainnya. Namun demikian, setiap pasang suami istri tidak berjabat tangan, maka banyaknya jabat tangan yang mungkin terjadi adalah ... .
A. $190$
B. $180$
C. $170$
D. $160$
E. $150$
A. $190$
B. $180$
C. $170$
D. $160$
E. $150$
Kunci : B. $180$
Petunjuk !
1. banyak cara dalam soal dapat dicari dengan menggunkan konsep permutasi atau kombinasi, dimana dalam soal orang A bersalaman dengan orang B merupakan kejadian yang sama jika B dan A berslaman. sehingga masalah ini dapat diselesaikan dengan permasalahan kombinasi.
2. pikirkan juga kasus suami istri yang tidak berjabat tangan dan ingat juga konsep kombinasi dimana $nCr=\frac{n!}{(n-r)!.r!)}$
Petunjuk !
1. banyak cara dalam soal dapat dicari dengan menggunkan konsep permutasi atau kombinasi, dimana dalam soal orang A bersalaman dengan orang B merupakan kejadian yang sama jika B dan A berslaman. sehingga masalah ini dapat diselesaikan dengan permasalahan kombinasi.
2. pikirkan juga kasus suami istri yang tidak berjabat tangan dan ingat juga konsep kombinasi dimana $nCr=\frac{n!}{(n-r)!.r!)}$
--- Soal No 3 ---
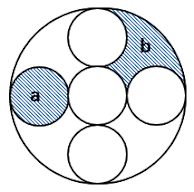
Jika kelima lingkaran kecil berjari-jari r dan titik-titik pusat lingkaran kecil yang menyinggung lingkaran besar merupakan titik-titik sudut suatu persegi. Jika nilai a adalah 10 $cm^2$ maka berapakah nilai b... .
A. $10$
B. $20$
C. $30$
D. $40$
E. $5$
B. $20$
C. $30$
D. $40$
E. $5$
Kunci : A. $10$
Petunjuk !
1. perhatikan hubungan jari-jari lingkaran kecil dan lingkaran besar, dari point ini akan ditemukan luas lingkaran besar.
2. luas lingkatan besar merupakan penjumlahan 5 lingkaran kecil ditambahkan 4 luas daerah arsiran b. Melalui persamaan ini nilai b akan ditemukan
3. soal selesai
Petunjuk !
1. perhatikan hubungan jari-jari lingkaran kecil dan lingkaran besar, dari point ini akan ditemukan luas lingkaran besar.
2. luas lingkatan besar merupakan penjumlahan 5 lingkaran kecil ditambahkan 4 luas daerah arsiran b. Melalui persamaan ini nilai b akan ditemukan
3. soal selesai
--- Soal No 4 ---
Diketahui persegi ABCD Dengan panjang sisi satu satuan panjang.Misalkan P adalah suatu titik di dalam sehingga besar sudut APB adalah $120^o$. Jumlah luas daerah seitiga APB dan segitiga CPD adalah ... .
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{5}{6}$
E. $\frac{2}{3}$
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{5}{6}$
E. $\frac{2}{3}$
Kunci : A. $\frac{1}{2}$
Petunjuk !
1. Ilustrasikan soap pada sebuah gambar, dan berikan semua ukuran yang diketahui pada soal.
2. ambil garis bantu yang melalui P dan memotong tegak lurus sisi AB dan DC misalkan memotong di titik Q dan R. kemudian misalkan panjang PQ = t dan PR = 1 -t, maka ini adala tinggi kedua segitiga yang ditanyakan.
3. selesaikan soal dengan mengingat konsep luas segitiga.
Petunjuk !
1. Ilustrasikan soap pada sebuah gambar, dan berikan semua ukuran yang diketahui pada soal.
2. ambil garis bantu yang melalui P dan memotong tegak lurus sisi AB dan DC misalkan memotong di titik Q dan R. kemudian misalkan panjang PQ = t dan PR = 1 -t, maka ini adala tinggi kedua segitiga yang ditanyakan.
3. selesaikan soal dengan mengingat konsep luas segitiga.
--- Soal No 5 ---
H adalah himpunan semua bilangan asli n sedemikin hingga bentuk $frac{n-1}{n-3}$ menghasilkan bilangan bulat kurang dari 1 banyaknya himpunan bagian tak kosong dari H adalah... .
A. $1$
B. $2$
C. $3$
D. $4$
E. $7$
A. $1$
B. $2$
C. $3$
D. $4$
E. $7$
Kunci : C. $3$
Petunjuk !
1. Jika H adalah himpunan dengan anggota n, maka banyak himpunan bagian dari H adalah $2^n$.
2. temukan semua nilai n sesuai dengan syarat pada soal, yaitu dengan memisahkan bentuk $frac{n-1}{n-3}$ menjadi bilangan bulat ditambahkan dengan suatu pecahan yang memuat penyebut n, temukan semua nilai n yang mungkin.
3. maka semua himpunan bagian dari H yang bukan himpunan kosong diperoleh dengan cara $2^n - 1$
Petunjuk !
1. Jika H adalah himpunan dengan anggota n, maka banyak himpunan bagian dari H adalah $2^n$.
2. temukan semua nilai n sesuai dengan syarat pada soal, yaitu dengan memisahkan bentuk $frac{n-1}{n-3}$ menjadi bilangan bulat ditambahkan dengan suatu pecahan yang memuat penyebut n, temukan semua nilai n yang mungkin.
3. maka semua himpunan bagian dari H yang bukan himpunan kosong diperoleh dengan cara $2^n - 1$
--- Soal No 6 ---
Dalam satu tahun harga mobil berkurang 10% dari harga tahun sebelumnya berapa tahun yang diperlukan agar harga mobil menjadi setengahnya dari harga awal ... .
A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
Kunci :E. $7$
Petunjuk !
1. ini merupakan permasalahan bungan majemuk, sehingga misalkan dulu harga awal adalah $a$ maka harga akhir yang diinginkan adalah $\frac{1}{2}a$. sehingga lama menagung diperoleh dengan cara menggunakan rumus $Ho=(1+b)^n.Ha$ dimana
Ho = Harga akhir
Ha = harga awal
b= besar bunga atau kerugian atau penyusutan
n = lama penyusutan, menabung atau lainnya.
2. maksukan semua nilai yang diketahui ke persamaan tersebut dan temukan nilai n.
Petunjuk !
1. ini merupakan permasalahan bungan majemuk, sehingga misalkan dulu harga awal adalah $a$ maka harga akhir yang diinginkan adalah $\frac{1}{2}a$. sehingga lama menagung diperoleh dengan cara menggunakan rumus $Ho=(1+b)^n.Ha$ dimana
Ho = Harga akhir
Ha = harga awal
b= besar bunga atau kerugian atau penyusutan
n = lama penyusutan, menabung atau lainnya.
2. maksukan semua nilai yang diketahui ke persamaan tersebut dan temukan nilai n.
--- Soal No 7 ---
Sebuah kotak piramida dibawah akan di isi dengan bilangan. Mula-mula yang harus diisikan adalah kotak-kotak pada alas piramid, dengan kotak diatasnya diperoleh dengan cara menjumlahkan bilangan pada kedua kotak dibawahnya. Andaikan piramid itu akan diisi dengan bilangan 7, 12, 5, 4 dan 9, maka berapakah nilai terbesar yang mungkin dari bilangan pada kotak yang paling atas .. .
A. $145$
B. $175$
C. $225$
D. $159$
E. $125$
B. $175$
C. $225$
D. $159$
E. $125$
Kunci : A. $145$
Petunjuk !
Agar nilai dipuncak piramida menjadi terbesar, maka bilangan paling bawah haruslah bilangan yang paling besar, temukan nilai nilai yang mungkin.
Petunjuk !
Agar nilai dipuncak piramida menjadi terbesar, maka bilangan paling bawah haruslah bilangan yang paling besar, temukan nilai nilai yang mungkin.
--- Soal No 8 ---
Bentuk sederhana dari
$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...\frac{1}{2005(2005+1)}$ adalah ... .
A. $\frac{2003}{2002}$
B. $\frac{2005}{2004}$
C. $\frac{2005}{2006}$
D. $\frac{2006}{2005}$
E. $\frac{2004}{2005}$
$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...\frac{1}{2005(2005+1)}$ adalah ... .
A. $\frac{2003}{2002}$
B. $\frac{2005}{2004}$
C. $\frac{2005}{2006}$
D. $\frac{2006}{2005}$
E. $\frac{2004}{2005}$
Kunci : C. $\frac{2005}{2006}$
Petunjuk !
1. jika bentuk - bentuk di dalam tanda kurung diubah ke dalam bentuk tertentu maka nilainya akan saling menghilangkan dengan bentuk di kurung lainnya. sehingga temukan kaitan/hubungan agar ada bentuk yang saling menghilangkan.
2. ubahlah bentuknya di dalam kurung ke bentuk pengurangan dua pecahan.
Petunjuk !
1. jika bentuk - bentuk di dalam tanda kurung diubah ke dalam bentuk tertentu maka nilainya akan saling menghilangkan dengan bentuk di kurung lainnya. sehingga temukan kaitan/hubungan agar ada bentuk yang saling menghilangkan.
2. ubahlah bentuknya di dalam kurung ke bentuk pengurangan dua pecahan.
--- Soal No 9 ---
Sebuah balok memiliki sisi-sisi yang luasnya $24 cm^3$, $32 cm^3$, dan $48 cm^3$, maka berapakah jumlah semua panjang sisi balok tersebut ... .
A. $72$
B. $66$
C. $64$
D. $74$
E. $75$
A. $72$
B. $66$
C. $64$
D. $74$
E. $75$
Kunci : A. $72$
Petunjuk !
1. dari informasi luas sisinya, temukan nilai volumenya dengan cara memisalkan ketiga luas dengan perkelian sisi-sisi balok. kemudian kalikan ketiga persamaan yang diperoleh.
2. jika volume sudah ada, maka jika volume dibagi dengan luas alas maka akan ditemukan tinggi balok, jika volume di bagi sisi samping-sampingnya maka akan ditemukan lebar dan panjangnya.
3. jumlahkan semua nilai rusuk pada kubus.
Petunjuk !
1. dari informasi luas sisinya, temukan nilai volumenya dengan cara memisalkan ketiga luas dengan perkelian sisi-sisi balok. kemudian kalikan ketiga persamaan yang diperoleh.
2. jika volume sudah ada, maka jika volume dibagi dengan luas alas maka akan ditemukan tinggi balok, jika volume di bagi sisi samping-sampingnya maka akan ditemukan lebar dan panjangnya.
3. jumlahkan semua nilai rusuk pada kubus.
--- Soal No 10 ---
Pompa air merk tangguh sanggup memompa sebanyak 25 liter setiap menit, pompa air merek perksa sanggup memompa air 400cc dalam setiap detik dan pompa air merek tahan banting sanggup memompa air sebanyak $1,6 m^3$ setiap jam. pompa air manakah yang paling cepat untuk mengisi sebuah tangki berukuran 500 liter... .
A. $Tangguh$
B. $Jujur$
C. $Perkasa$
D. $Tahan$
E. $Tahan Banting$
A. $Tangguh$
B. $Jujur$
C. $Perkasa$
D. $Tahan$
E. $Tahan Banting$
Kunci : E. $Tahan Banting$
Petunjuk !
1. temukan debit setiap merek pompa dengan satuan yang sama, ingatlah konsep tangga pengukuran volume.
2. ingat juga kesetaraan cc dengan liter dengan meter kubik
3. jika sudah disamakan maka pilih yang paing cepat
Petunjuk !
1. temukan debit setiap merek pompa dengan satuan yang sama, ingatlah konsep tangga pengukuran volume.
2. ingat juga kesetaraan cc dengan liter dengan meter kubik
3. jika sudah disamakan maka pilih yang paing cepat







Tidak ada komentar:
Posting Komentar