| Berikut disajikan soal Olimpiade Matematika SMP yang dikumpulkan dari berbagai sumber, baik dari buku, internet, menanyakan ke peserta lomba atau dari sumber lainnya. Dalam penyajiannya juga disertakan petunjuk cara pengerjaan, kunci dan video pembahasan di setiap soalnya, Hal ini dimaksudkan agar siswa bisa mengerjakan soal sesuai dengan kebutuhannya serta Semoga postingan ini dapat membatu siswa menuju medali olimpiade yang sudah didambakan. |
--- Soal No 1 ---
Dengan menggunkan angka-angka 1, 1, 2, 2, 3, 3, 4, 4 akan dibuat bilangan 8 angka denga syarat angka 1 dipisahkan oleh satu angka yang lain, kedua angka 2 dipisahkan oleh dua angka 3 dipisahkan oleh tiga angka dan kedua anka 4 dipisahkan dengan empat angka, bilangan terbesar yang dapat dibentuk adalah ... .
A. $41312432$
B. $41312432$
C. $42312413$
D. $44332211$
E. $43211234$
A. $41312432$
B. $41312432$
C. $42312413$
D. $44332211$
E. $43211234$
Kunci : A. $41312432$
Petunjuk !
Susunlah angka-angka pada soal sesuai dengan syratnya dan akan menjadi angka paling besar jika angka 4 dijadikan bilangan pertama. Temukan susunanya.
Petunjuk !
Susunlah angka-angka pada soal sesuai dengan syratnya dan akan menjadi angka paling besar jika angka 4 dijadikan bilangan pertama. Temukan susunanya.
--- Soal No 2 ---
Hasil kali suatu bilangan genap dan ganji adalah 840. Bilangan ganjil terbesar yang memenuhi syarat tersebut adalah ... .
A. $105$
B. $35$
C. $841$
D. $21$
E. $85$
A. $105$
B. $35$
C. $841$
D. $21$
E. $85$
Kunci : A. $105$
Petunjuk !
Temukan faktorisasi prima dari angka 840, kemudian carilah kombinasi bilangan ganjil yang ditimbulkan oleh faktorisasi prima dari bilangan 840.
Petunjuk !
Temukan faktorisasi prima dari angka 840, kemudian carilah kombinasi bilangan ganjil yang ditimbulkan oleh faktorisasi prima dari bilangan 840.
--- Soal No 3 ---
Persegi dibawah ini memiliki satu satuan luas, Pecahan yang menyatakan luas daerah yang tidak diarsir adalah … .
A. $\frac{3}{8}$
B. $\frac{8}{3}$
C. $\frac{3}{16}$
D. $\frac{16}{3}$
E. $\frac{1}{2}$
C. $\frac{3}{16}$
D. $\frac{16}{3}$
E. $\frac{1}{2}$
Kunci : A. $\frac{3}{8}$
Petunjuk !
Perhatikan, daerah yang diarsir adalah daerah segitiga. Maka unutk mencari pecahan yang menyatakan luas daerah yang tidak diarsir dapat dilakukan dengan menemukan selisih persegi dengan daerah yang diarsir dimana daerah yang diarsir dibentuk oleh 4 buah segitiga.
Petunjuk !
Perhatikan, daerah yang diarsir adalah daerah segitiga. Maka unutk mencari pecahan yang menyatakan luas daerah yang tidak diarsir dapat dilakukan dengan menemukan selisih persegi dengan daerah yang diarsir dimana daerah yang diarsir dibentuk oleh 4 buah segitiga.
--- Soal No 4 ---
Semua nilai n sehingga $\frac{n+3}{n-1}$ merupakan bilangan bulat … .
A. $(-3, -1, 0, 2, 3, 5.)$
B. $(-3, 1, 0, 2, 3, 5.)$
C. $(-3, -1, 0, 1, 2, 3, 5.)$
D. $(-3, -1, 0, 3, 5.)$
E. $(-3, -1, 2, 3, 5.)$
A. $(-3, -1, 0, 2, 3, 5.)$
B. $(-3, 1, 0, 2, 3, 5.)$
C. $(-3, -1, 0, 1, 2, 3, 5.)$
D. $(-3, -1, 0, 3, 5.)$
E. $(-3, -1, 2, 3, 5.)$
Kunci : ada 6 yaitu -3, -1, 0, 2, 3, 5.
Petunjuk !
1. Ubahlah bentuk $\frac{n+3}{n-1}$ menjadi sembarang bilangan bulat dijumlahkan atau dikurangi dengan pecahan yang pembilangnya adalah bilangan bulat dan penyebutnya n – 1. sehingga jika sudah ketemu akan memudahkan menemukan solusi bulat yang dimaksudkan oleh soal.
2. Temukan semua kemungkian yang terjadi.
Petunjuk !
1. Ubahlah bentuk $\frac{n+3}{n-1}$ menjadi sembarang bilangan bulat dijumlahkan atau dikurangi dengan pecahan yang pembilangnya adalah bilangan bulat dan penyebutnya n – 1. sehingga jika sudah ketemu akan memudahkan menemukan solusi bulat yang dimaksudkan oleh soal.
2. Temukan semua kemungkian yang terjadi.
--- Soal No 5 ---
Misalkan diketahui $N = \frac{1}{10} + \frac{1}{10^2} + \frac{1}{10^3} +...+ \frac{1}{10^{11}}$ Dalam bentuk desimal nilai N adalah …
A. $0,123456798011$
B. $0,123456799011$
C. $0,123456789011$
D. $0,123457689011$
E. $0,123456879011$
A. $0,123456798011$
B. $0,123456799011$
C. $0,123456789011$
D. $0,123457689011$
E. $0,123456879011$
Kunci : C. $0,123456789011$
Petunjuk !
Ubahlah nilai pecahan menjadi desimal kemudian jumlahkan.
Petunjuk !
Ubahlah nilai pecahan menjadi desimal kemudian jumlahkan.
--- Soal No 6 ---
Sebuah tempat air berbentuk kerucut. Untuk mengisi tempat air itu dengan air sampai pada ketinggian $\frac{1}{2}$ t diperlukan sebanyak 38,5 liter. Volume air berbentuk kerucut tersebut adalah … .
A. $307$
B. $308$
C. $309$
D. $310$
E. $311$
A. $307$
B. $308$
C. $309$
D. $310$
E. $311$
Kunci : B. $308$
Petunjuk !
1. Temukan nilai jari – jari kerucut dengan konsep kesebangunan segitiga.
2. Temukan nilai jari jari yang disebabkan oleh permukaan air dari nilai volume yang diketahui dalam soal.
3. soal dapat diselesaikan.
Petunjuk !
1. Temukan nilai jari – jari kerucut dengan konsep kesebangunan segitiga.
2. Temukan nilai jari jari yang disebabkan oleh permukaan air dari nilai volume yang diketahui dalam soal.
3. soal dapat diselesaikan.
--- Soal No 7 ---
Jika $2^{13}$ dibagi dengan 13 akan memberikan sisa …
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Kunci : A. $\frac{175}{4}$
Petunjuk !
1. Temukan bilangan abc sehingga berlaku a.b + c = 213. Sehingga nilai c adalah sisa pembagianya.
2. Soal juga dapat diselesaikan dengan konsep modulo.
Petunjuk !
1. Temukan bilangan abc sehingga berlaku a.b + c = 213. Sehingga nilai c adalah sisa pembagianya.
2. Soal juga dapat diselesaikan dengan konsep modulo.
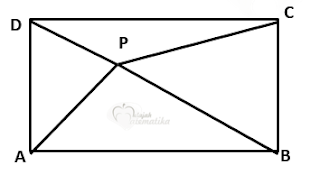
--- Soal No 8 ---
A. $12$
B. $13$
C. $14$
D. $15$
E. $16$
B. $13$
C. $14$
D. $15$
E. $16$
Kunci : A. $12$
Petunjuk !
1. Buatlah 2 garis bantu yang melalui P yang masing-masing sejajar dengan AB dan CD.
2. Melalui garis bantu akan ditemukan 4 pasang segitiga kongruen, melalui segitiga tersebut temukan persamaan menggunakan konsep pytagoras.
3. Selesaikan persamaan yang diperoleh.
Petunjuk !
1. Buatlah 2 garis bantu yang melalui P yang masing-masing sejajar dengan AB dan CD.
2. Melalui garis bantu akan ditemukan 4 pasang segitiga kongruen, melalui segitiga tersebut temukan persamaan menggunakan konsep pytagoras.
3. Selesaikan persamaan yang diperoleh.
--- Soal No 9 ---
Rata – rata sembilan bilangan adalah 6, satu data diantaranya dibuang maka rata-ratanya menjadi 6,5 berapakah bilangan yang dibuang … .
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Kunci : B. $2$
Petunjuk !
1. Temukan selisih jumlah data sebelum dan sesudah dibuang.
2. gunakan konsep rata-rata gabungan dalam menemukan jawabannya.
Petunjuk !
1. Temukan selisih jumlah data sebelum dan sesudah dibuang.
2. gunakan konsep rata-rata gabungan dalam menemukan jawabannya.
--- Soal No 10 ---
Jumlah semua angka pada bilangan $2^{2004}.5^{2003}$ adalah … .
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Kunci : B. $2$
Petunjuk !
1. Ingatlah konsep bilangan berpangkat, yaitu jika $a^n.b^n = (a.b)^n$
2. pecah dan samakan pangkat bilangan, maka jika pangkatnya sudah sama maka bilangan basisnya bisa dikalikan.
3. selesaikan soal.
Petunjuk !
1. Ingatlah konsep bilangan berpangkat, yaitu jika $a^n.b^n = (a.b)^n$
2. pecah dan samakan pangkat bilangan, maka jika pangkatnya sudah sama maka bilangan basisnya bisa dikalikan.
3. selesaikan soal.
--- Soal No 11 ---
Joko mengalikan tiga bilangan prima berbeda sekaligus. Ada berapa faktor berbeda yang dihasilkan bilangan itu ... .
A. $3$
B. $4$
C. $5$
D. $6$
E. $8$
A. $3$
B. $4$
C. $5$
D. $6$
E. $8$
Kunci :E. $8$
Petunjuk !
1. Ingatlah konsep bahwa Jika faktoriasai suatu bilangan n adalah $n={p_{1}}^{_{a_1}}.{p_{2}}^{_{a_2}}. ... .{p_{n}}^{_{a_n}}$ maka banyak faktor dari n adalah $(a_1+1)(a_2+1). ... (a_n+1)$
2. atau jika kesusahan bisa menemukan pola yang dibentuk perkalian dua bilangan, tiga bilangan 4 bilangan prima.
3. gunakan salah satu konsep diatas, maka soal dapat diselesaikan.
Petunjuk !
1. Ingatlah konsep bahwa Jika faktoriasai suatu bilangan n adalah $n={p_{1}}^{_{a_1}}.{p_{2}}^{_{a_2}}. ... .{p_{n}}^{_{a_n}}$ maka banyak faktor dari n adalah $(a_1+1)(a_2+1). ... (a_n+1)$
2. atau jika kesusahan bisa menemukan pola yang dibentuk perkalian dua bilangan, tiga bilangan 4 bilangan prima.
3. gunakan salah satu konsep diatas, maka soal dapat diselesaikan.
--- Soal No 12 ---
Alex selalu berbohong pada hari-hari kamis, jumat dan sabtu. Pada hari lain ales selalu berkata jurjur, Dilain pihak Frans selalu berbohong pada hari minggu, senin dan selasa dan selalu jujur pada hari lainnya. Pada suatu hari keduanya berkata "kemarin saya berbohong", maka hari apa mereka mengucapkan kata itu ... .
A. $Jumat$
B. $Sabtu$
C. $Minggu$
D. $Senin$
E. $Selasa$
A. $Jumat$
B. $Sabtu$
C. $Minggu$
D. $Senin$
E. $Selasa$
Kunci : C. $Minggu$
Petunjuk !
1. list/cacah semua kemungkinan ia berkata seperti itu, dan baliklah kata yang diucapkan jika ia berbohong.
2. akan ada 1 hari dimana salah satu diantara mereka berbohong dan salah satu yang lain berkata jujur sesuai pernyataan dengan soal.
Petunjuk !
1. list/cacah semua kemungkinan ia berkata seperti itu, dan baliklah kata yang diucapkan jika ia berbohong.
2. akan ada 1 hari dimana salah satu diantara mereka berbohong dan salah satu yang lain berkata jujur sesuai pernyataan dengan soal.







Tidak ada komentar:
Posting Komentar