--- Soal No 1 ---
Fungsi kuadrat $f(x) = ax^2 - (2a- 4)x + (a +4)$ selalu bernilai positif unfuk nilai a yang memenuhi ....
A. $a \geq 2$
B. $a > 2$
C. $a \geq \frac{1}{2}$
D. $a > \frac{1}{2}$
E. $a > 0$
A. $a \geq 2$
B. $a > 2$
C. $a \geq \frac{1}{2}$
D. $a > \frac{1}{2}$
E. $a > 0$
Kunci : D. $a > \frac{1}{2}$
Petunjuk :
1. selalu bernilai positif memiliki makna tidak ada nilai x yang menyebabkan nilai fungsi negatif atau fungsi tidak memotong sumbu x
2. bernilai selalu positif sering disebut dengan definit positif dan selalu bernilai negatif sering disebut definit negatif
3. definit negatif terjadi saat $D<0$ dan $a <0$ sedangkan definit positif terjadi saat $D < 0$ dan $a > 0$
Petunjuk :
1. selalu bernilai positif memiliki makna tidak ada nilai x yang menyebabkan nilai fungsi negatif atau fungsi tidak memotong sumbu x
2. bernilai selalu positif sering disebut dengan definit positif dan selalu bernilai negatif sering disebut definit negatif
3. definit negatif terjadi saat $D<0$ dan $a <0$ sedangkan definit positif terjadi saat $D < 0$ dan $a > 0$
--- Soal No 2 ---
Fungsi kuadrat $y=ax^2+x+a$ definit negatif untuk konstanta a yang memenuhi ...
A. $a < -\frac{1}{2}$ atau $a <\frac{1}{2}$
B. $-\frac{1}{2} < a < \frac{1}{2}$
C. $0 < a < \frac{1}{2}$
D. $a < 0$
E. $a < -\frac{1}{2}$
A. $a < -\frac{1}{2}$ atau $a <\frac{1}{2}$
B. $-\frac{1}{2} < a < \frac{1}{2}$
C. $0 < a < \frac{1}{2}$
D. $a < 0$
E. $a < -\frac{1}{2}$
Kunci : E. $a < -\frac{1}{2}$
Petunjuk :
1. selalu bernilai positif memiliki makna tidak ada nilai x yang menyebabkan nilai fungsi negatif atau fungsi tidak memotong sumbu x
2. bernilai selalu positif sering disebut dengan definit positif dan selalu bernilai negatif sering disebut definit negatif
3. definit negatif terjadi saat $D<0$ dan $a <0$ sedangkan definit positif terjadi saat $D < 0$ dan $a > 0$
Petunjuk :
1. selalu bernilai positif memiliki makna tidak ada nilai x yang menyebabkan nilai fungsi negatif atau fungsi tidak memotong sumbu x
2. bernilai selalu positif sering disebut dengan definit positif dan selalu bernilai negatif sering disebut definit negatif
3. definit negatif terjadi saat $D<0$ dan $a <0$ sedangkan definit positif terjadi saat $D < 0$ dan $a > 0$
--- Soal No 3 ---
Grafik fungsi $f(x) = x^2- 6x + 7$ dapat diperoleh dengan cara menggeser grafik fungsi
$f(x) = x^2$ ke arah ....
A. Kanan sumbu X sejauh 2 satuan dan ke arah bawah sumbu Y sejauh 3 satuan.
B. Kiri sumbu X sejauh 3 satuan dan ke arah atas sumbu Y sejauh 2 satuan.
C. Kanan sumbu X sejauh 3 satuan dan ke arah bawah sumbu Y sejauh 2 satuan
D. Kanan sumbu X sejauh 6 satuan dan ke arah bawah sumbu Y sejauh 7 satuan.
E. iri sumbu X sej auh 2 satuan dan ke arah atas sumbu Y sejauh 3 satuan.
A. Kanan sumbu X sejauh 2 satuan dan ke arah bawah sumbu Y sejauh 3 satuan.
B. Kiri sumbu X sejauh 3 satuan dan ke arah atas sumbu Y sejauh 2 satuan.
C. Kanan sumbu X sejauh 3 satuan dan ke arah bawah sumbu Y sejauh 2 satuan
D. Kanan sumbu X sejauh 6 satuan dan ke arah bawah sumbu Y sejauh 7 satuan.
E. iri sumbu X sej auh 2 satuan dan ke arah atas sumbu Y sejauh 3 satuan.
Kunci : C. Kanan sumbu X sejauh 3 satuan dan ke arah bawah sumbu Y sejauh 2 satuan
Petunjuk :
1. untuk melihat pergeseran suatu grafik maka bentuk fungsi dapat diubah ke bentuk $f(x)=(x-a)^2+b$ yang memiliki makna bahwa fungsi digeser a satuan ke kanan atau kiri dan b satuan ke atas atau bawah. tanda menandakan kemana arah gesernya
2. ubahlah bentuk fungsi pada soal sesuai bentuk fungsi pada point 1
Petunjuk :
1. untuk melihat pergeseran suatu grafik maka bentuk fungsi dapat diubah ke bentuk $f(x)=(x-a)^2+b$ yang memiliki makna bahwa fungsi digeser a satuan ke kanan atau kiri dan b satuan ke atas atau bawah. tanda menandakan kemana arah gesernya
2. ubahlah bentuk fungsi pada soal sesuai bentuk fungsi pada point 1
--- Soal No 4 ---
Diketahui $f(x) = (x - a)(x - b)$ dengan $a,b$ dan $x$ bilangan real dan $a < b$. Pernyataan berikut ini yang benar adalah . . .
A. Jika $ab=0$, maka $f(x)=0$ untuk setiap $x$
B. Jika $x < a$ maka $f(x) <0$
C. Jika $a < x < b$ maka $f(x) > 0$
D. Jika $a < x < b$ maka $f(x) < 0$
E. Jika $x <$ maka $f(x) > 0$
A. Jika $ab=0$, maka $f(x)=0$ untuk setiap $x$
B. Jika $x < a$ maka $f(x) <0$
C. Jika $a < x < b$ maka $f(x) > 0$
D. Jika $a < x < b$ maka $f(x) < 0$
E. Jika $x <$ maka $f(x) > 0$
Kunci : D. Jika $a < x < b$ maka $f(x) < 0$
Petunjuk :
1. perhatikan bentuk $f(x) = (x - a)(x - b)$ ini menandakan bahwa kedua akarnya adalah bilangan bulat fositif.
2. jika dilihat bentuk grafik yang akan ditimbulkan oleh persamaan tesebut maka di sebelah kiri $x=a$ fungsi selalu positif, dan disebelah kanan $x=b$ juga selalu positif sedangkan diantara $x=a$ dan $x=b$ nilai fungsi selalu negatif
3. berdasarkan informasi diatas cocokan jawaban yang tepat.
Petunjuk :
1. perhatikan bentuk $f(x) = (x - a)(x - b)$ ini menandakan bahwa kedua akarnya adalah bilangan bulat fositif.
2. jika dilihat bentuk grafik yang akan ditimbulkan oleh persamaan tesebut maka di sebelah kiri $x=a$ fungsi selalu positif, dan disebelah kanan $x=b$ juga selalu positif sedangkan diantara $x=a$ dan $x=b$ nilai fungsi selalu negatif
3. berdasarkan informasi diatas cocokan jawaban yang tepat.
--- Soal No 5 ---
Fungsi $f$ dan $g$ disebut saling simetris jika grafik f dapat diperoleh dengan mencerminkan grafik g terhadap sumbu X. semua pasangan fungsi berikut saling simetris, KECUALI ... .
A. $f(x)=x^2-2$ dan $g(x)=x^2+1$
B. $f(x)=(x-2)^2-2$ dan $g(x)=2-(x-2)^2$
C. $f(x)=4x-x^2$ dan $g(x)=x^2-4x$
D. $f(x)=sinx$ dan $g(x)=-sinx$
E. $f(x)=x^2-2$ dan $g(x)=2-x^2$
A. $f(x)=x^2-2$ dan $g(x)=x^2+1$
B. $f(x)=(x-2)^2-2$ dan $g(x)=2-(x-2)^2$
C. $f(x)=4x-x^2$ dan $g(x)=x^2-4x$
D. $f(x)=sinx$ dan $g(x)=-sinx$
E. $f(x)=x^2-2$ dan $g(x)=2-x^2$
Kunci : A. $f(x)=x^2-2$ dan $g(x)=x^2+1$
Petunjuk :
1. sesuai syarat simetris pada soal maka $g(x)=-f(x)$
2. temukan semua fungsi yang memiliki aturan seperti aturan pada point 1.
Petunjuk :
1. sesuai syarat simetris pada soal maka $g(x)=-f(x)$
2. temukan semua fungsi yang memiliki aturan seperti aturan pada point 1.
--- Soal No 6 ---
Fungsi $f(x)=x^2+ax$ mempunyai grafik berikut.
Grafik fungsi $g(x) = x^2-ax-5$ adalah ...
| A. | B. | C. |
| D. | E. |
Kunci : C
Petunjuk :
1. perhatikan bentuk grafik $g(x) = x^2-ax-5$, sesuai konsepnya grafik akan memotong sumbu y di titik $(0,-5)$. maka cocokan grafi yang sesuai
2. sesuai point 1 jawaban yang mungkin adalah C dan D namun jawaban D kurang tepat karena grafik pada jawaban D memiliki simetri $x=0$ sementara simetri dari $g(x) = x^2-ax-5$ tidak mungkin di $x=0$
Petunjuk :
1. perhatikan bentuk grafik $g(x) = x^2-ax-5$, sesuai konsepnya grafik akan memotong sumbu y di titik $(0,-5)$. maka cocokan grafi yang sesuai
2. sesuai point 1 jawaban yang mungkin adalah C dan D namun jawaban D kurang tepat karena grafik pada jawaban D memiliki simetri $x=0$ sementara simetri dari $g(x) = x^2-ax-5$ tidak mungkin di $x=0$
--- Soal No 7 ---
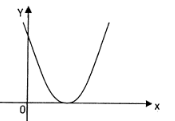
Grafik fungsi $y=ax^2+bx+c$ ditunjukan di bawah ini
pernyataan yang benar adalah ... .
A. $ab > 0$ dan $a+b+c >0$
B. $ab < 0$ dan $a+b+c >0$
C. $ab > 0$ dan $a+b+c \leq 0$
D. $ab < 0$ dan $a+b+c <0$
E. $ab < 0$ dan $a+b+c \geq 0$
pernyataan yang benar adalah ... .
A. $ab > 0$ dan $a+b+c >0$
B. $ab < 0$ dan $a+b+c >0$
C. $ab > 0$ dan $a+b+c \leq 0$
D. $ab < 0$ dan $a+b+c <0$
E. $ab < 0$ dan $a+b+c \geq 0$
Kunci : A. $ab > 0$ dan $a+b+c >0$
Petunjuk :
1. hal pertama yang dapat dilihat adalah nilai a yang selalu positif karena grafik terbuka keatas.
2. nilai b diperoleh dengan cara menemukan sumbu simetri kurva, dengan cara $x=\frac{-b}{2a}$ dimana sumbu simetrinya terletak di x yang negatif
3. nilai c diperoleh dari tipot dengan sumbu y, dimana tiotnya di sumbu y positif.
4. temukan jawaban yang tepat sesuai ketiga informasi diatas.
Petunjuk :
1. hal pertama yang dapat dilihat adalah nilai a yang selalu positif karena grafik terbuka keatas.
2. nilai b diperoleh dengan cara menemukan sumbu simetri kurva, dengan cara $x=\frac{-b}{2a}$ dimana sumbu simetrinya terletak di x yang negatif
3. nilai c diperoleh dari tipot dengan sumbu y, dimana tiotnya di sumbu y positif.
4. temukan jawaban yang tepat sesuai ketiga informasi diatas.
--- Soal No 8 ---
Jika grafik fungsi kuadrat $f(x) : ax^2 + bx + c$ dengan titik puncak $(5,-4)$ memotong sumbu X positif dan sumbu Y negatif, maka ... .
A. $a-c > 0$
B. $a+c < 0$
C. $a+c=0$
D. $a+c > 0$
E. $a-c < 0$
A. $a-c > 0$
B. $a+c < 0$
C. $a+c=0$
D. $a+c > 0$
E. $a-c < 0$
Kunci : A. $a-c > 0$
Petunjuk :
1. jika diilustrasikan sesuai pada soal, maka diperoleh kurva erbuka ke atas.
2. dari gambar, karena grafik terbuka keats maka nilai $a >0$ kemudian nilai c negatif karena c adalah tipot dengan sumbu y
3. nilai b juga diperoleh dengan cara melihat nilai sumbu simetrinya.
4. temukan hubungan nilai a,b dan c unutk menjawab soalnya
Petunjuk :
1. jika diilustrasikan sesuai pada soal, maka diperoleh kurva erbuka ke atas.
2. dari gambar, karena grafik terbuka keats maka nilai $a >0$ kemudian nilai c negatif karena c adalah tipot dengan sumbu y
3. nilai b juga diperoleh dengan cara melihat nilai sumbu simetrinya.
4. temukan hubungan nilai a,b dan c unutk menjawab soalnya
--- Soal No 9 ---
Jika fungsi kuadrat f memiliki,sifat-sifat : $f (x) \geq 0$ untuk semua bilangan real $x, f(1) = 0$ dan $f(2) = 2$, maka nilai $f(0) + f (4)$ adalah . ...
A. $25$
B. $20$
C. $15$
D. $10$
E. $5$
A. $25$
B. $20$
C. $15$
D. $10$
E. $5$
Kunci : B. $20$
Petunjuk :
1. temukan fungsi kuadratnya, dengan rumus membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ dimana persamannya diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2.pada soal nilai puncak ada sembarang titik juga ada.
3. temukan nilai fungsi yang ditanyakan pada soal.
Petunjuk :
1. temukan fungsi kuadratnya, dengan rumus membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ dimana persamannya diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2.pada soal nilai puncak ada sembarang titik juga ada.
3. temukan nilai fungsi yang ditanyakan pada soal.
--- Soal No 10 ---
Suatu grafik fungsi kuadrat $f$ dengan titik puncak $(-2,-1)$ dan melalui titik $(0,-5)$, maka nilai $f(2)$ adalah ... .
A. $-17$
B. $-18$
C. $-19$
D. $-20$
E. $-21$
A. $-17$
B. $-18$
C. $-19$
D. $-20$
E. $-21$
Kunci : A. $-17$
Petunjuk :
1. membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2. pada soal jelas nilai puncak dan sembarang titiknya, maka temukan nilai $a$ pada point 1 terlebih dahulu
3. jika nilai a sudah ada maka rumus pada point 1 digunakan kembali dan ubah nilai a dan nilai titik puncaknya.
Petunjuk :
1. membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2. pada soal jelas nilai puncak dan sembarang titiknya, maka temukan nilai $a$ pada point 1 terlebih dahulu
3. jika nilai a sudah ada maka rumus pada point 1 digunakan kembali dan ubah nilai a dan nilai titik puncaknya.
--- Soal No 11 ---
Suatu grafik fungsi kuadrat / dengan titik puncak $(-2,0)$ dan melalui titik $(0,-4)$, maka nilai $f (-5)$ adalah ...
A. $-7$
B. $-8$
C. $-9$
D. $-10$
E. $-11$
A. $-7$
B. $-8$
C. $-9$
D. $-10$
E. $-11$
Kunci : C. $-9$
Petunjuk :
1. membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2. pada soal jelas nilai puncak dan sembarang titiknya, maka temukan nilai $a$ pada point 1 terlebih dahulu
3. jika nilai a sudah ada maka rumus pada point 1 digunakan kembali dan ubah nilai a dan nilai titik puncaknya.
Petunjuk :
1. membuat persamaan kuadrat jika nilai puncak di $(x_p,y_p)$ dan melalui sembarang titik $(x,y)$ diperoleh dengan cara $y_p=a(x-x_p)^2+y_p$
2. pada soal jelas nilai puncak dan sembarang titiknya, maka temukan nilai $a$ pada point 1 terlebih dahulu
3. jika nilai a sudah ada maka rumus pada point 1 digunakan kembali dan ubah nilai a dan nilai titik puncaknya.
--- Soal No 12 ---
Jika $f$ adalah fungsi kuadrat yang grafiknya melalui titik $(-1,0), (2,0)$ dan $(0,2)$, maka nilai $f(-7)$ adalah ... .
A. $-8$
B. $-16$
C. $-24$
D. $-32$
E. $-40$
A. $-8$
B. $-16$
C. $-24$
D. $-32$
E. $-40$
Kunci : E. $-40$
Petunjuk :
1. perhatikan ketiga titik yang diberikan pada soal, disana diketahui 2 titik yang memotong sumbu x sehingga untuk menemukan fungsi grafiknya dapat ditemukan dengan cara $y=a(x-x_1)(x-x_2)$
2. Temukan nilai a dengan mengganti titik puncaknya dan titik yang melalui grafik tersebut.
3. temukan persamaanya dengan rumus yang sama dengan mengganti titik puncaknya saja.
5. unutk menemukan nilai $f(5)$ maka ganti nilai x pada persamaan yang ditemukan dengan 7.
Petunjuk :
1. perhatikan ketiga titik yang diberikan pada soal, disana diketahui 2 titik yang memotong sumbu x sehingga untuk menemukan fungsi grafiknya dapat ditemukan dengan cara $y=a(x-x_1)(x-x_2)$
2. Temukan nilai a dengan mengganti titik puncaknya dan titik yang melalui grafik tersebut.
3. temukan persamaanya dengan rumus yang sama dengan mengganti titik puncaknya saja.
5. unutk menemukan nilai $f(5)$ maka ganti nilai x pada persamaan yang ditemukan dengan 7.
--- Soal No 13 ---
Jika grafik fungsi kuadrat $f(x)=ax^2+bx+c$ mempunyai titik puncak $(8,4)$ dan memotong sumbu x negatif maka ... .
A. $a > 0, b > 0$ dan $c>0$
B. $a < 0, b < 0$ dan $c>0$
C. $a < 0, b > 0$ dan $c<0$
D. $a > 0, b > 0$ dan $c<0$
E. $a < 0, b > 0$ dan $c>0$
A. $a > 0, b > 0$ dan $c>0$
B. $a < 0, b < 0$ dan $c>0$
C. $a < 0, b > 0$ dan $c<0$
D. $a > 0, b > 0$ dan $c<0$
E. $a < 0, b > 0$ dan $c>0$
Kunci : E. $a < 0, b > 0$ dan $c>0$
Petunjuk :
1. ilustrasikan gambar sesuai syarat pada soal
2. jika diperhatikan lesbih seksama, maka akan diperoleh kesimpulan bahwa nilai c lebih dari nol, nilai b diperoleh dengan sumbu simteri kurva dan nilai a pasti negatif karena kurva terbuka kebawah.
3. untuk menemukan nilai simetri suatu grafik diperoleh dengan cara $x=\frac{-b}{2a}$
4. pilih jawaban sesuai dengan pernyataan tersebut.
Petunjuk :
1. ilustrasikan gambar sesuai syarat pada soal
2. jika diperhatikan lesbih seksama, maka akan diperoleh kesimpulan bahwa nilai c lebih dari nol, nilai b diperoleh dengan sumbu simteri kurva dan nilai a pasti negatif karena kurva terbuka kebawah.
3. untuk menemukan nilai simetri suatu grafik diperoleh dengan cara $x=\frac{-b}{2a}$
4. pilih jawaban sesuai dengan pernyataan tersebut.
--- Soal No 14 ---
Fungsi kuadrat $f(x)=x^2+2px+p$ mempunyai nilai minimum $-p$ dengan $p \neq 0$. Jika sumbu simetri kurva $f$ adalah $x=a$, maka nilai $a+f(a)$ adalah ... .
A. $6$
B. $4$
C. $-4$
D. $-5$
E. $-6$
A. $6$
B. $4$
C. $-4$
D. $-5$
E. $-6$
Kunci : C. $-4$
Petunjuk :
1. temukan persamaan dalam bentuk p melalui nilai maksimum yang diketahui pada soal.
2. untuk menemukan nilai maksimum suatu fungsi maka diperoleh dengan cara $\frac{D}{-4a} atau bisa juga mensubstutusikan nilai simetrinya ke persamaan awal.
Petunjuk :
1. temukan persamaan dalam bentuk p melalui nilai maksimum yang diketahui pada soal.
2. untuk menemukan nilai maksimum suatu fungsi maka diperoleh dengan cara $\frac{D}{-4a} atau bisa juga mensubstutusikan nilai simetrinya ke persamaan awal.
--- Soal No 15 ---
Untuk $0 < a < 10$ fungsi kuadrat $f(x)=ax^2+2ax+10$ memiliki sifat
A. selalu negatif
B. selalu positif
C. hanya positif disetiap $x$ dengan $0 < x < 10$
D. hanya negatif disetiap $x$ dengan $0 < x < 10$
E. hanya positif disetiap $x$ dengan $x < 0$ atau $x > 10$
A. selalu negatif
B. selalu positif
C. hanya positif disetiap $x$ dengan $0 < x < 10$
D. hanya negatif disetiap $x$ dengan $0 < x < 10$
E. hanya positif disetiap $x$ dengan $x < 0$ atau $x > 10$
Kunci : B. selalu positif
Petunjuk :
1. ingat untuk menemukan sifat fungsi kuadrat sangat erat kaitanya dengan nilai diskriminan fungsi.
2. temukan nilai diskriminan fungsi pada soal yang akan ditemukan dalam variabel a, temukan nilai a yang mungkin
3. uji daerah yang disebabkan oleh nilai a tersebut. dan lihat bagaimana tandanya dalam rentang yang dimaksudkan.
Petunjuk :
1. ingat untuk menemukan sifat fungsi kuadrat sangat erat kaitanya dengan nilai diskriminan fungsi.
2. temukan nilai diskriminan fungsi pada soal yang akan ditemukan dalam variabel a, temukan nilai a yang mungkin
3. uji daerah yang disebabkan oleh nilai a tersebut. dan lihat bagaimana tandanya dalam rentang yang dimaksudkan.
--- Soal No 16 ---
Jika grafik fungsi $y = x^2 - 9$ memotong sumbu x di titik A dan B, serta memotong sumbu $y$ di titik C, maka luas segitiga ABC adalah ....
A. $36$
B. $33$
C. $30$
D. $27$
E. $24$
A. $36$
B. $33$
C. $30$
D. $27$
E. $24$
Kunci : D. $27$
Petunjuk :
1. ilustrasikan soal ke dalam gambar
2. titik ABC akan mebentuk sebuah segitiga sama kaki dengan ukuran alas dan tingginya langsung ditemukan.
3. temukan luas segitiga dengan konsep biasanya.
Petunjuk :
1. ilustrasikan soal ke dalam gambar
2. titik ABC akan mebentuk sebuah segitiga sama kaki dengan ukuran alas dan tingginya langsung ditemukan.
3. temukan luas segitiga dengan konsep biasanya.
--- Soal No 17 ---
Banyak parabola $Ax^2+Cy=0$ dengan $A$ dan $C$ dua bilangan berbeda dari ${0,1,4,16}$ adalah ... .
A. $10$
B. $8$
C. $6$
D. $4$
E. $3$
A. $10$
B. $8$
C. $6$
D. $4$
E. $3$
Kunci : D. $4$
Petunjuk :
1. ingatlah agar fungsi $Ax^2+Cy=0$ A atau C tidak boleh 0 sehingga temukan semua pasangan parabola yang mungkin dibentuk oleh angka 1, 4, 16
2. jika ditemukan akan ada 6 pasangan yang mungkin dan jika diuji akan ditemukan ada beberapa nilai kurva yang memiliki fungsi sama.
3. jika sama angap 1 kemungkinan.
Petunjuk :
1. ingatlah agar fungsi $Ax^2+Cy=0$ A atau C tidak boleh 0 sehingga temukan semua pasangan parabola yang mungkin dibentuk oleh angka 1, 4, 16
2. jika ditemukan akan ada 6 pasangan yang mungkin dan jika diuji akan ditemukan ada beberapa nilai kurva yang memiliki fungsi sama.
3. jika sama angap 1 kemungkinan.
--- Soal No 18 ---
Nilai konstanta positif a yang mungkin sehingga $\frac{457}{50}$ merupakan nilai minimum dari fungsi $f(x)=(a^2+1)x^2-2ax+10$ untuk x pada rentang $0$ sampai $\frac{1}{2}$ adalah ... .
A. $7$
B. $5$
C. $4$
D. $3$
E. $2$
A. $7$
B. $5$
C. $4$
D. $3$
E. $2$
Kunci : A. $7$
Petunjuk :
1. untuk menemukan nilai maksimum suatu fungsi maka diperoleh dengan cara $\frac{D}{-4a}$ atau bisa juga mensubstutusikan nilai simetrinya ke persamaan awal.
2. dengan pernyataan pada point 1 akan ditemukan sebuah persamaan dalam variabel a, maka selesaikanlah persamaan tersebut.
Petunjuk :
1. untuk menemukan nilai maksimum suatu fungsi maka diperoleh dengan cara $\frac{D}{-4a}$ atau bisa juga mensubstutusikan nilai simetrinya ke persamaan awal.
2. dengan pernyataan pada point 1 akan ditemukan sebuah persamaan dalam variabel a, maka selesaikanlah persamaan tersebut.













Tidak ada komentar:
Posting Komentar